Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify: (-4p^(3))^(3)

Simplify:\newline(−4p3)3(-4p^{3})^{3}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Add, subtract, multiply, and divide polynomialsright chevron icon

Full solution

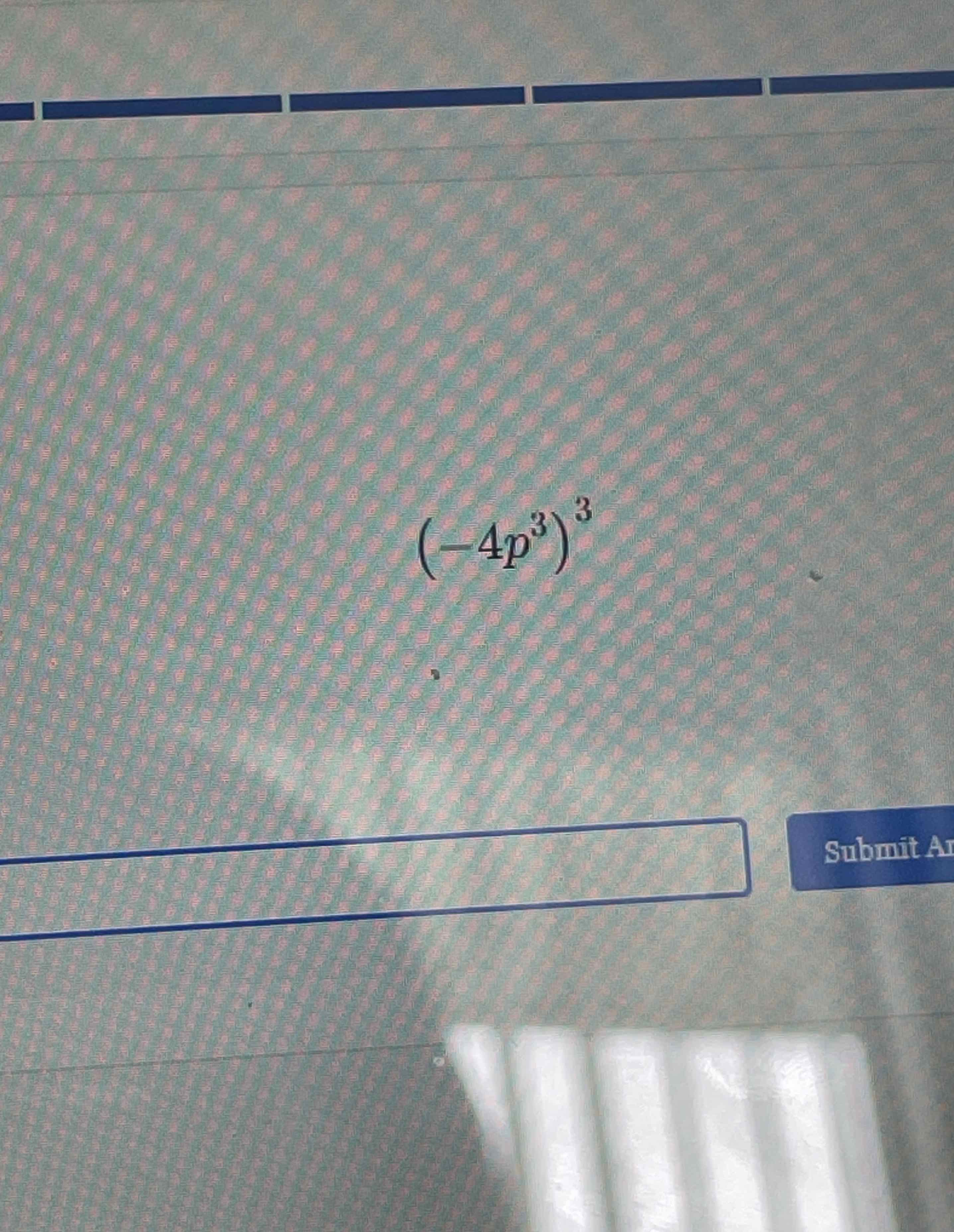
Q. Simplify:\newline(−4p3)3(-4p^{3})^{3}
  1. Recognize and Apply Power Rule: Step 11: Recognize the expression and apply the power rule for exponents. (−4p3)3=(−4)3×(p3)3(-4p^{3})^{3} = (-4)^{3} \times (p^{3})^{3}
  2. Calculate Cube of −4-4: Step 22: Calculate the cube of −4-4.(−4)3=−64(-4)^3 = -64
  3. Apply Power Rule to (p3)3(p^3)^3: Step 33: Apply the power rule to (p3)3(p^3)^3.(p3)3=p(3∗3)=p9(p^3)^3 = p^{(3*3)} = p^9
  4. Combine Results: Step 44: Combine the results from Step 22 and Step 33.\newline−64×p9=−64p9-64 \times p^9 = -64p^9

More problems from Add, subtract, multiply, and divide polynomials

Question
Find the solutions of the quadratic equation 2x2−8x−9=0 2 x^{2}-8 x-9=0 .\newlineChoose 11 answer:\newline(A) 2±342i 2 \pm \frac{\sqrt{34}}{2} i \newline(B) −2±342i -2 \pm \frac{\sqrt{34}}{2} i \newline(C) 2±342 2 \pm \frac{\sqrt{34}}{2} \newline(D) 1±344 1 \pm \frac{\sqrt{34}}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for x x .\newlineEnter the solutions from least to greatest.\newline(−5x+4)(x−3)=0 lesser x=□ greater x=□ \begin{array}{l} (-5 x+4)(x-3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for x x .\newlineEnter the solutions from least to greatest.\newline(2x+4)(3x−2)=0 (2 x+4)(3 x-2)=0 \newlinelesser x= x= \newlinegreater x= x=
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for x x .\newlineEnter the solutions from least to greatest.\newline(3x−6)(−x+3)=0 lesser x=□ greater x=□ \begin{array}{l} (3 x-6)(-x+3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for x x .\newlineEnter the solutions from least to greatest.\newline(x+6)(−x+1)=0 (x+6)(-x+1)=0 \newlinelesser x= x= \newlinegreater x= x=
Get tutor helpright-arrow

Posted 4 months ago

Question
Is the following function even, odd, or neither?\newlinef(x)=3x2+2 f(x)=\frac{3}{x^{2}+2} \newlineChoose 11 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither
Get tutor helpright-arrow

Posted 4 months ago

Question
Is the following function even, odd, or neither?\newlinef(x)=14−x2 f(x)=\frac{1}{4-x^{2}} \newlineChoose 11 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither
Get tutor helpright-arrow

Posted 4 months ago

Question
Is the following function even, odd, or neither?\newlinef(x)=2∣x∣−5 f(x)=2|x|-5 \newlineChoose 11 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither
Get tutor helpright-arrow

Posted 4 months ago

Question
Is the following function even, odd, or neither?\newlinef(x)=xx2+1 f(x)=\frac{x}{x^{2}+1} \newlineChoose 11 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither
Get tutor helpright-arrow

Posted 4 months ago

Question
Is the following function even, odd, or neither?\newlinef(x)=x3−4x f(x)=x^{3}-4 x \newlineChoose 11 answer:\newline(A) Even\newline(B) Odd\newline(C) Neither
Get tutor helpright-arrow

Posted 4 months ago

View all (62)