Full solution
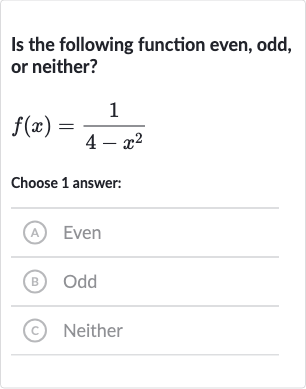
Q. Is the following function even, odd, or neither?Choose answer:(A) Even(B) Odd(C) Neither
- Define function and find f(-x): Define the function f(x) and find f(-x).The function given is . To determine if the function is even, odd, or neither, we need to evaluate and compare it to .Substitute for in to get .
- Simplify : Simplify .Simplify the expression inside the parentheses.Since , we have:
- Compare and : Compare and .We have and .Since , the function is an even function.