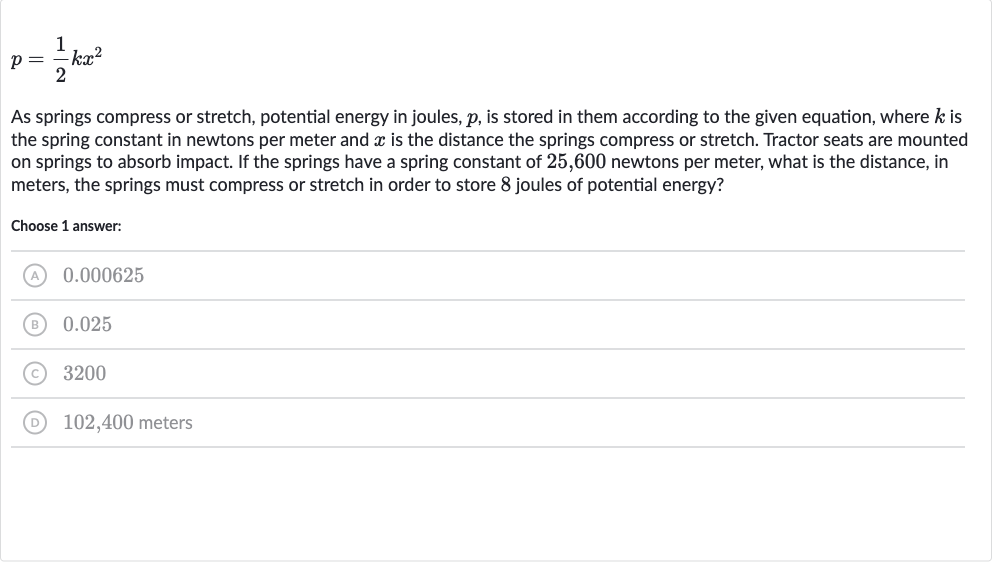
$p=\frac{1}{2} k x^{2}$ $\newline$ As springs compress or stretch, potential energy in joules, $p$ , is stored in them according to the given equation, where $k$ is the spring constant in newtons per meter and $x$ is the distance the springs compress or stretch. Tractor seats are mounted on springs to absorb impact. If the springs have a spring constant of $25$ , $600$ newtons per meter, what is the distance, in meters, the springs must compress or stretch in order to store $8$ joules of potential energy? $\newline$ Choose $1$ answer: $\newline$ (A) $0$ . $000625$ $\newline$ (B) $0$ . $025$ $\newline$ (C) $3200$ $\newline$ (D) $102$ , $400$ meters

Full solution

p=\frac{1}{2} k x^{2}

\newline

As springs compress or stretch, potential energy in joules,

p

, is stored in them according to the given equation, where

k

is the spring constant in newtons per meter and

x

is the distance the springs compress or stretch. Tractor seats are mounted on springs to absorb impact. If the springs have a spring constant of

25

600

newtons per meter, what is the distance, in meters, the springs must compress or stretch in order to store

8

joules of potential energy?

\newline

Choose

1

answer:

\newline

(A)

0

000625

\newline

(B)

0

025

\newline

(C)

3200

\newline

(D)

102

400

meters

Substitute values into equation: Plug in the given values for $p$ and $k$ into the equation $p = \frac{1}{2}kx^2$ to solve for $x$ . $p = 8$ joules, $k = 25,600$ N/m. $8 = \frac{1}{2}(25,600)x^2$ .
Eliminate fraction: Multiply both sides by $2$ to get rid of the fraction. $\newline$ $2 \times 8 = 25,600x^2$ . $\newline$ $16 = 25,600x^2$ .
Solve for $x^2$ : Divide both sides by $25,600$ to solve for $x^2$ .
$\frac{16}{25,600} = x^2$ .
$0.000625 = x^2$ .
Find final value of $\newline$ $x$ : Take the square root of both sides to solve for $\newline$ $x$ . $\newline$ $\newline$ $x = \sqrt{0.000625}$ . $\newline$ $\newline$ $x = 0.025$ meters.