Let h(x)=2x^(3)+3x^(2)-12 x+5". " The absolute minimum value of h over the closed interval -3

Question

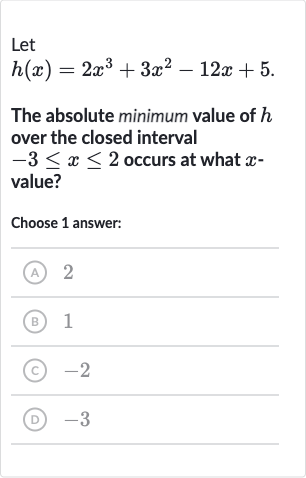
Let  h(x)=2x^(3)+3x^(2)-12 x+5". " The absolute minimum value of  h over the closed interval  -3 <= x <= 2 occurs at what  x value? Choose 1 answer: (A) 2 (B) 1 (C) -2 (D) -3

Bytelearn · Accepted Answer

Calculate Derivative of h(x): To find the absolute minimum value of the function h(x) on the closed interval [-3, 2], we need to find the critical points of h(x) within the interval and evaluate h(x) at the endpoints of the interval. Critical points occur where the derivative h'(x) is zero or undefined. First, we calculate the derivative of h(x). h'(x) = d/dx [2x^3 + 3x^2 - 12x + 5]        = 6x^2 + 6x - 12Find Critical Points: Next, we find the critical points by setting the derivative equal to zero and solving for x. 6x^2 + 6x - 12 = 0 Divide by 6 to simplify: x^2 + x - 2 = 0 Factor the quadratic equation: (x + 2)(x - 1) = 0 So, the critical points are x = -2 and x = 1.Evaluate Function at Points: Now we need to evaluate the function h(x) at the critical points and at the endpoints of the interval, x = -3 and x = 2. h(-3) = 2(-3)^3 + 3(-3)^2 - 12(-3) + 5       = -54 + 27 + 36 + 5       = 14 h(-2) = 2(-2)^3 + 3(-2)^2 - 12(-2) + 5       = -16 + 12 + 24 + 5       = 25 h(1) = 2(1)^3 + 3(1)^2 - 12(1) + 5      = 2 + 3 - 12 + 5      = -2 h(2) = 2(2)^3 + 3(2)^2 - 12(2) + 5      = 16 + 12 - 24 + 5      = 9Identify Absolute Minimum: Comparing the values of h(x) at the critical points and endpoints, we find that the smallest value is h(1) = -2. Therefore, the absolute minimum value of h(x) over the interval [-3, 2] occurs at x = 1.

Let $h(x)=2 x^{3}+3 x^{2}-12 x+5 \text {. }$ $\newline$ The absolute minimum value of $h$ over the closed interval $-3 \leq x \leq 2$ occurs at what $x$ value? $\newline$ Choose $1$ answer: $\newline$ (A) $2$ $\newline$ (B) $1$ $\newline$ (C) $-2$ $\newline$ (D) $-3$

Full solution

More problems from Conjugate root theorems

Related topics