Full solution
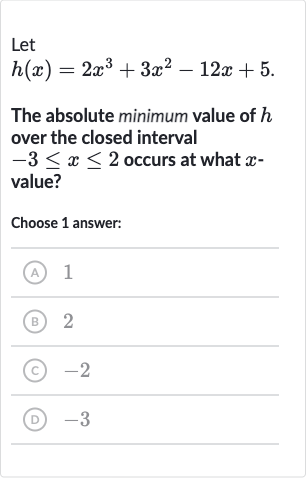
Q. Let The absolute minimum value of over the closed interval occurs at what value?Choose answer:(A) (B) (C) (D)
- Calculate Derivative of : To find the absolute minimum value of the function on the closed interval , we need to find the critical points of within the interval and evaluate at the endpoints of the interval. Critical points occur where the derivative is zero or undefined.
- Find Critical Points: First, we calculate the derivative of :
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :. To simplify the equation, we can divide by :.
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :. To simplify the equation, we can divide by :.We factor the quadratic equation:. This gives us two critical points: and .
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and .
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and ..
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and ...
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and ....
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and .....
- Evaluate at Points: Next, we find the critical points by setting to zero and solving for :.To simplify the equation, we can divide by :.We factor the quadratic equation:.This gives us two critical points: and .Now we evaluate at the critical points and at the endpoints of the interval:, , , and .....Comparing the values of at the critical points and endpoints, we find that the absolute minimum value occurs at , since is the smallest value.