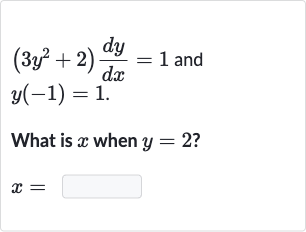Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3y^(2)+2)(dy)/(dx)=1 and
y(-1)=1.
What is
x when
y=2 ?

x=

$\left(3 y^{2}+2\right) \frac{d y}{d x}=1$ and $y(-1)=1$ . $\newline$ What is $x$ when $y=2$ ? $\newline$ $x=$

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

Q.

\left(3 y^{2}+2\right) \frac{d y}{d x}=1

and

y(-1)=1

.

\newline

What is

x

when

y=2

?

\newline

x=

Separate variables: First, we need to separate the variables to integrate both sides of the differential equation. So we get \frac{dy}{\(3\)y^{\(2\)}+\(2\)} = \frac{dx}{\(1\)}\.
Integrate both sides: Now, integrate both sides. The integral of \(\frac{dy}{3y^{2}+2} with respect to $y$ is the integral of $dx$ with respect to $x$ .
Find constant of integration: The integral of $\frac{dy}{3y^{2}+2}$ is $\frac{1}{3} \cdot \arctan\left(\frac{y}{\sqrt{2/3}}\right) + C$ , and the integral of $dx$ is $x$ .
Solve for C: We need to find the constant of integration $C$ using the initial condition $y(-1)=1$ . So we plug in $y=1$ and $x=-1$ into the integrated equation: $(-\frac{1}{3}) \cdot \arctan(\frac{1}{\sqrt{\frac{2}{3}}}) + C = -1$ .
Particular solution: Solve for $C$ . $C = -1 + \left(\frac{1}{3}\right) \cdot \arctan\left(\sqrt{\frac{3}{2}}\right)$ .
Find $x$ when $y=2$ : Now we have the particular solution. We need to find $x$ when $y=2$ . Plug $y=2$ into the integrated equation: $(1/3) \cdot \arctan(2/\sqrt{2/3}) + C = x$ .
Substitute $C$ into equation: Substitute the value of $C$ we found earlier into the equation: $x = \left(\frac{1}{3}\right) * \arctan\left(\frac{2}{\sqrt{\frac{2}{3}}}\right) - 1 + \left(\frac{1}{3}\right) * \arctan\left(\sqrt{\frac{3}{2}}\right)$ .
Calculate x: Now, calculate the value of $x$ . $x \approx \left(\frac{1}{3}\right) * \text{arctan}\left(2*\sqrt{\frac{3}{2}}\right) - 1 + \left(\frac{1}{3}\right) * \text{arctan}\left(\sqrt{\frac{3}{2}}\right)$ .

More problems from Find the roots of factored polynomials

Question

Find the solutions of the quadratic equation

2 x^{2}-8 x-9=0

\newline

1

\newline

2 \pm \frac{\sqrt{34}}{2} i

\newline

-2 \pm \frac{\sqrt{34}}{2} i

\newline

2 \pm \frac{\sqrt{34}}{2}

\newline

1 \pm \frac{\sqrt{34}}{4}

Posted 3 months ago

Question

x^{3}+7 x^{2}-36

\newline

The polynomial has zeros at

-6

2

. If the remaining zero is

z

, then what is the value of

-z

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

\begin{array}{l} (-5 x+4)(x-3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

(2 x+4)(3 x-2)=0

\newline

x=

\newline

x=

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

\begin{array}{l} (3 x-6)(-x+3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

(x+6)(-x+1)=0

\newline

x=

\newline

x=

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{3}{x^{2}+2}

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{1}{4-x^{2}}

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=2|x|-5

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{x}{x^{2}+1}

\newline

1

\newline

\newline

\newline

Posted 3 months ago