Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

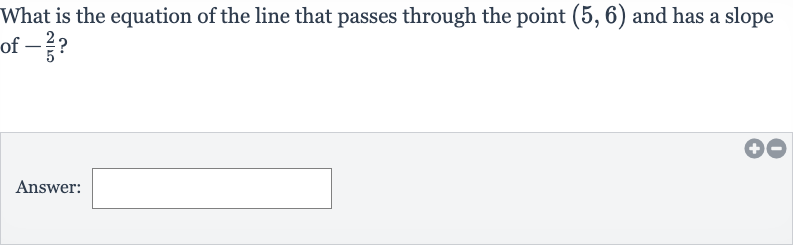
What is the equation of the line that passes through the point (5,6) and has a slope of -(2)/(5) ? Answer:

What is the equation of the line that passes through the point (5,6) (5,6) and has a slope of −25 -\frac{2}{5} ?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

Q. What is the equation of the line that passes through the point (5,6) (5,6) and has a slope of −25 -\frac{2}{5} ?\newlineAnswer:
  1. Identify Point-Slope Form: To find the equation of a line, we can use the point-slope form of a line, which is given by y−y1=m(x−x1)y - y_1 = m(x - x_1), where mm is the slope and (x1,y1)(x_1, y_1) is a point on the line.
  2. Substitute Values: Given the point (5,6)(5,6) and the slope m=−25m = -\frac{2}{5}, we can substitute these values into the point-slope form equation: y−6=−25(x−5)y - 6 = -\frac{2}{5}(x - 5).
  3. Distribute Slope: Now we will distribute the slope −25-\frac{2}{5} across the (x−5)(x - 5) term: y−6=−25x+25⋅5y - 6 = -\frac{2}{5}x + \frac{2}{5}\cdot 5.
  4. Simplify Equation: Simplify the equation by multiplying 25\frac{2}{5} by 55, which gives us 22: y−6=−25x+2y - 6 = -\frac{2}{5}x + 2.
  5. Isolate y: Next, we will add 66 to both sides of the equation to solve for yy: y=−25x+2+6y = -\frac{2}{5}x + 2 + 6.
  6. Combine Terms: Combine the constant terms on the right side of the equation: y=−25x+8y = -\frac{2}{5}x + 8.

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant