AI tutor
Full solution
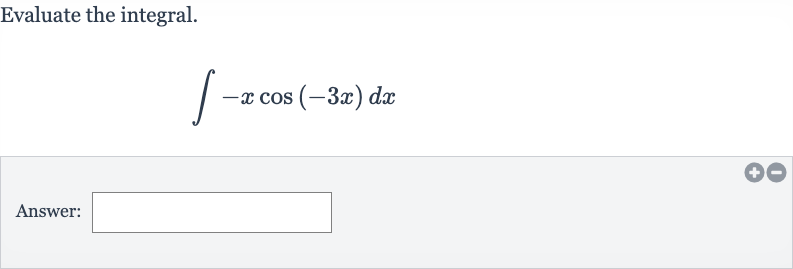
Q. Evaluate the integral.Answer:
- Write Integral: Write down the integral to be solved.
- Factor Out Constant: Use the property of integrals that , where is a constant, to factor out the constant from the integral.
- Apply Even Property: Recognize that due to the even property of the cosine function.
- Apply Integration by Parts: Apply integration by parts, where and . Then we need to find and .Let , so .Let , so , since the integral of is .
- Integrate : Apply the integration by parts formula: .I = -\left(x \cdot \left(\frac{\(1\)}{\(3\)}\right)\sin(\(3x) - \int\left(\frac{}{}\right)\sin(x) \, dx\right)
- Simplify and Combine: Integrate with respect to . The integral of is , so the integral of is .
- Factor Out Constants: Simplify the expression and combine like terms., where is the constant of integration.
- Factor Out Constants: Simplify the expression and combine like terms., where is the constant of integration.Factor out the constants to make the expression cleaner.