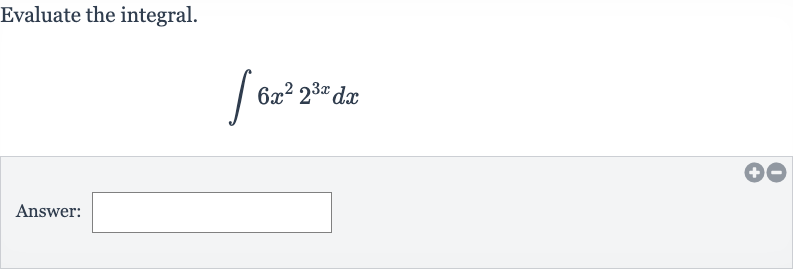
Evaluate the integral. int6x^(2)2^(3x)dx Answer:

Question

Evaluate the integral.  int6x^(2)2^(3x)dx Answer:

Bytelearn · Accepted Answer

Identify integral: Identify the integral to be solved. We need to evaluate the integral of the function 6x^2 * 2^(3x) with respect to x. I = ∫6x^2 * 2^(3x) dxRecognize integral type: Recognize that the integral involves a product of a polynomial and an exponential function. This integral does not have a straightforward antiderivative, so we will need to use integration by parts. Integration by parts formula: ∫u dv = uv - ∫v duChoose u and dv: Choose u and dv. Let u = 6x^2 (which will become simpler when differentiated) and dv = 2^(3x) dx (which will remain the same when integrated).Differentiate and integrate: Differentiate u and integrate dv. du = d(6x^2) = 12x dx v = ∫2^(3x) dx To integrate v, we need to use the fact that ∫a^(f(x)) f'(x) dx = a^(f(x))/ln(a) + C, where a is a constant and f(x) is a function of x.Integrate dv to find v: Integrate dv to find v. v = ∫2^(3x) dx = 2^(3x)/(3ln(2)) + CApply integration by parts: Apply the integration by parts formula. I = uv - ∫v du I = (6x^2) * (2^(3x)/(3ln(2))) - ∫(2^(3x)/(3ln(2))) * (12x) dxSimplify the expression: Simplify the expression. I = (2x^2 * 2^(3x))/(ln(2)) - (4/ln(2)) * ∫x * 2^(3x) dx Now we have a new integral to solve, which is again a product of a polynomial and an exponential function.Apply integration by parts again: Apply integration by parts to the new integral. Let u = x and dv = 2^(3x) dx for the new integral. du = dx v = ∫2^(3x) dx = 2^(3x)/(3ln(2)) + C (as calculated before)Integrate new integral: Apply the integration by parts formula to the new integral. I_new = uv - ∫v du I_new = x * (2^(3x)/(3ln(2))) - ∫(2^(3x)/(3ln(2))) dxApply integration by parts to new integral: Integrate the remaining integral. ∫(2^(3x)/(3ln(2))) dx = (2^(3x)/(9ln(2)^2)) + CIntegrate remaining integral: Substitute I_new back into the original integral. I = (2x^2 * 2^(3x))/(ln(2)) - (4/ln(2)) * (x * (2^(3x)/(3ln(2))) - (2^(3x)/(9ln(2)^2)))Substitute I_new: Simplify the expression. I = (2x^2 * 2^(3x))/(ln(2)) - (4x * 2^(3x))/(3ln(2)^2) + (4 * 2^(3x))/(9ln(2)^3) + CSimplify the expression: Combine the terms and write the final answer. I = (2x^2 * 2^(3x))/(ln(2)) - (4x * 2^(3x))/(3ln(2)^2) + (4 * 2^(3x))/(9ln(2)^3) + C

Evaluate the integral. $\newline$ $\int 6 x^{2} 2^{3 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x ∫6x223xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int 6 x^{2} 2^{3 x} d x$ $\newline$ Answer: