AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral.Answer:
Full solution
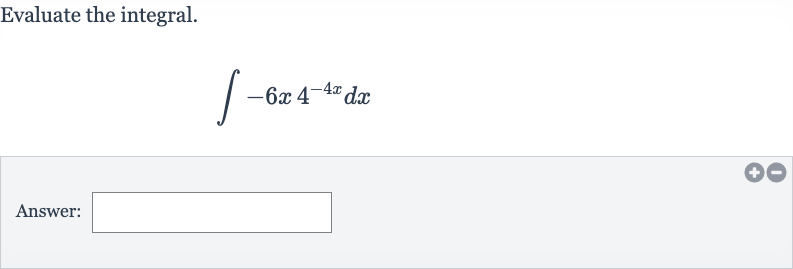
Q. Evaluate the integral.Answer:
- Define Integral: Let's denote the integral we want to evaluate as :To solve this integral, we will use integration by parts, which states that , where and are differentiable functions of . We need to choose and such that the resulting integral is easier to solve. Let's choose: (which means ) (which means we need to find )To find , we need to integrate . Since is an exponential function, we can use the fact that when and . In our case, and , so .
- Integration by Parts: Now we integrate to find :
Using the formula for integrating an exponential function with a linear exponent, we get:
We can simplify this by multiplying the numerator and denominator by : - Choose and : Now that we have and , we can apply the integration by parts formula:Substituting , , and into the formula, we get:Simplifying the integral, we get:
- Find v: We have already integrated when finding v, so we can use that result here:Simplifying the expression, we get:
- Apply Integration by Parts: Now we can combine the terms with a common base of :$I = \(4\)^{\(-4\)x}\left(\frac{\(3\)x}{\(2\)\ln(\(4\))} - \frac{\(3\)}{\(8\)\ln(\(4\))^\(2\)}\right)
- Simplify Integral: Finally, we add the constant of integration \(C\) to our result:\(\newline\)\(I = 4^{-4x}\left(\frac{3x}{2\ln(4)} - \frac{3}{8\ln(4)^2}\right) + C\)\(\newline\)This is the indefinite integral of the given function.
