AI tutor
Full solution
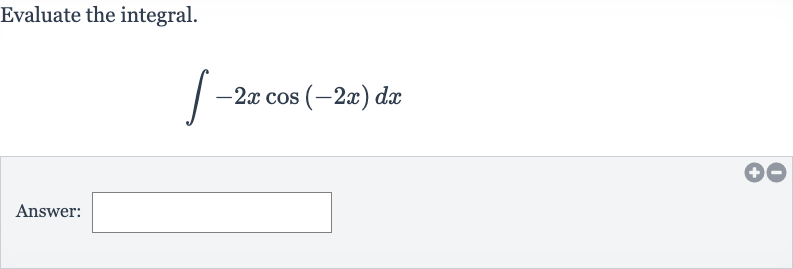
Q. Evaluate the integral.Answer:
- Simplify Integral: Let's first simplify the integral by using the property of cosine that . This simplifies our integral to:Now we can proceed with integration by parts, where we let and . Then we need to find and .Differentiating with respect to gives us , and integrating gives us , since the integral of is .
- Integration by Parts: Now we apply the integration by parts formula:Substituting our chosen , , , and , we get:Simplifying the right side, we have:
- Integrate : Next, we integrate . The integral of with respect to is , so we have:where is the constant of integration.
- Combine Terms: Now we combine the terms to get the final answer: simplifies toThis is our final answer.