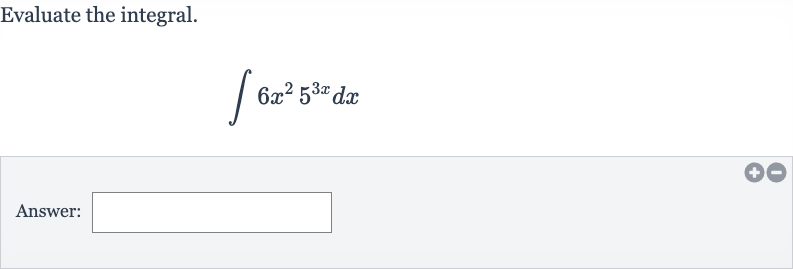AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral.Answer:
Full solution
Q. Evaluate the integral.Answer:
- Choose and : To solve the integral of with respect to , we will use integration by parts, which is given by the formula . We need to choose and such that the resulting integral is simpler to solve.Let's choose (which will simplify when differentiated) and (which we can integrate).
- Differentiate : Differentiate to find . Using the power rule, , so .
- Integrate dv: Integrate to find . This is an exponential function, and we can integrate it by using the formula , where is the base of the exponential and is the coefficient of .$v = \int \(6\) \cdot \(5\)^{\(3\)x} \, dx = \left(\frac{\(6\)}{\(3\)\ln(\(5\))}\right) \cdot \(5\)^{\(3\)x} = \left(\frac{\(2\)}{\ln(\(5\))}\right) \cdot \(5\)^{\(3\)x}.
- Apply integration by parts: Now apply the integration by parts formula: \(\int u \, dv = uv - \int v \, du\). Substitute \(u = x^2\), \(du = 2x \, dx\), and \(v = \left(\frac{2}{\ln(5)}\right) \cdot 5^{3x}\) into the formula. \(\int 6x^{2}5^{3x} \, dx = x^2 \cdot \left(\frac{2}{\ln(5)}\right) \cdot 5^{3x} - \int \left(\frac{2}{\ln(5)}\right) \cdot 5^{3x} \cdot 2x \, dx\).
- Simplify expression: Simplify the expression and prepare to integrate the second term.\(\newline\)\(\int 6x^{2}5^{3x} dx = \left(\frac{2x^2}{\ln(5)}\right) * 5^{3x} - \left(\frac{4}{\ln(5)}\right) * \int x * 5^{3x} dx.\)\(\newline\)Now we need to integrate \(\int x * 5^{3x} dx\), which again requires integration by parts.
- Choose \(u\) and \(dv\): For the new integration by parts, let's choose \(u = x\) (which will simplify when differentiated) and \(dv = 5^{3x} dx\) (which we can integrate).\(\newline\)Differentiate \(u = x\) to find \(du\). Using the power rule, \(\frac{du}{dx} = 1\), so \(du = dx\).\(\newline\)Integrate \(dv = 5^{3x} dx\) to find \(v\). Using the same exponential integration formula as before, \(dv\)\(0\).
- Differentiate \(u\): Apply the integration by parts formula to the integral \(\int x \cdot 5^{3x} \, dx\).\(\int x \cdot 5^{3x} \, dx = x \cdot \frac{5^{3x}}{3\ln(5)} - \int \frac{5^{3x}}{3\ln(5)} \, dx\).
- Integrate dv: Integrate the remaining term \(\int\frac{5^{3x}}{3\ln(5)} dx\). This is a simple exponential integral.\(\newline\)\(\int\frac{5^{3x}}{3\ln(5)} dx = \frac{5^{3x}}{9\ln(5)^2} + C\), where \(C\) is the constant of integration.
- Apply integration by parts: Substitute the integrated parts back into the original integration by parts expression. \(\int \(6\)x^{\(2\)}\(5\)^{\(3\)x} \, dx = \left(\frac{\(2\)x^\(2\)}{\ln(\(5\))}\right) * \(5\)^{\(3\)x} - \left(\frac{\(4\)}{\ln(\(5\))}\right) * \left(\frac{x * (\(5\)^{\(3\)x})}{\(3\)\ln(\(5\))} - \frac{\(5\)^{\(3\)x}}{\(9\)\ln(\(5\))^\(2\)}\right) + C.
- Integrate remaining term: Simplify the expression by distributing and combining like terms. \(\int \(6\)x^{\(2\)}\(5\)^{\(3\)x} \, dx = \left(\frac{\(2\)x^\(2\)}{\ln(\(5\))}\right) \cdot \(5\)^{\(3\)x} - \left(\frac{\(4\)x}{\(3\)\ln(\(5\))^\(2\)}\right) \cdot \(5\)^{\(3\)x} + \left(\frac{\(4\)}{\(9\)\ln(\(5\))^\(3\)}\right) \cdot \(5\)^{\(3\)x} + C.
- Substitute integrated parts: Combine the terms with the common factor of \(5^{3x}\). \(\newline\)\[\int 6x^{2}5^{3x} \, dx = 5^{3x} \left( \frac{2x^2}{\ln(5)} - \frac{4x}{3\ln(5)^2} + \frac{4}{9\ln(5)^3}\right) + C.\]
