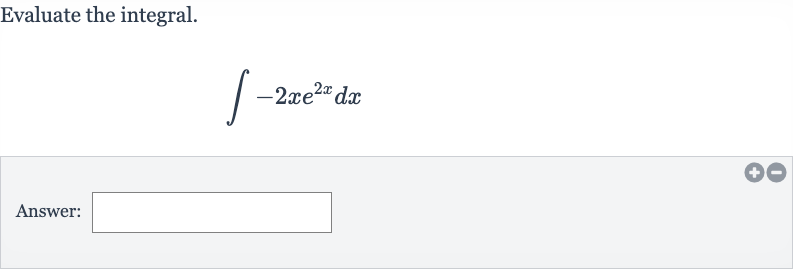
Evaluate the integral. int-2xe^(2x)dx Answer:

Question

Evaluate the integral.  int-2xe^(2x)dx Answer:

Bytelearn · Accepted Answer

Identify integral: Identify the integral to be solved. We need to evaluate the integral of the function -2xe^(2x) with respect to x. I = ∫-2xe^(2x)dxUse integration by parts: Use integration by parts. Integration by parts formula is ∫u dv = uv - ∫v du, where u and dv are parts of the integrand. Let u = -2x (which will be differentiated) and dv = e^(2x)dx (which will be integrated).Differentiate and integrate: Differentiate u and integrate dv. Differentiating u with respect to x gives us du = -2dx. Integrating dv with respect to x gives us v = (1/2)e^(2x), since the integral of e^(ax) is (1/a)e^(ax) and here a = 2.Apply integration by parts: Apply the integration by parts formula. Now we have u = -2x, du = -2dx, v = (1/2)e^(2x). Using the integration by parts formula, we get: I = uv - ∫v du I = (-2x)(1/2)e^(2x) - ∫(1/2)e^(2x)(-2dx)Simplify expression: Simplify the expression. I = -xe^(2x) - ∫-e^(2x)dx Now we need to integrate -e^(2x) with respect to x.Integrate -e^(2x): Integrate -e^(2x) with respect to x. The integral of -e^(2x) is -1/2e^(2x), since the integral of e^(ax) is (1/a)e^(ax) and here a = 2.Combine and add constant: Combine the results and add the constant of integration. I = -xe^(2x) - (-1/2)e^(2x) + C I = -xe^(2x) + (1/2)e^(2x) + CWrite final answer: Write the final answer. The integral of -2xe^(2x) with respect to x is: I = -xe^(2x) + (1/2)e^(2x) + C

Evaluate the integral. $\newline$ $\int-2 x e^{2 x} d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x ∫−2xe2xdx\newlineAnswer:

Evaluate the integral. $\newline$ $\int-2 x e^{2 x} d x$ $\newline$ Answer: