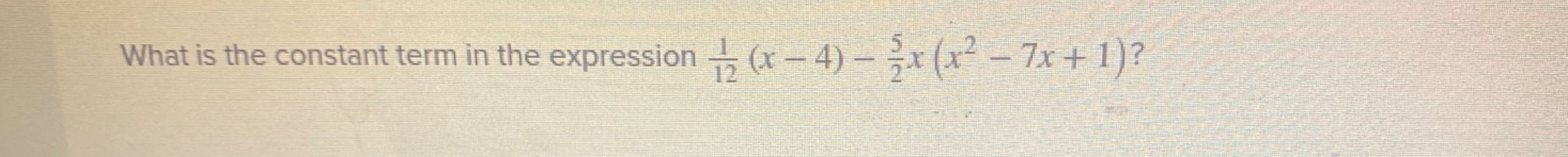AI tutor
Full solution
Q. What is the constant term in the expression ?
- Distribute and Combine Terms: Simplify the expression by distributing and combining like terms. =
- Combine Like Terms: Combine like terms to simplify further.Combine the terms and constant terms separately.