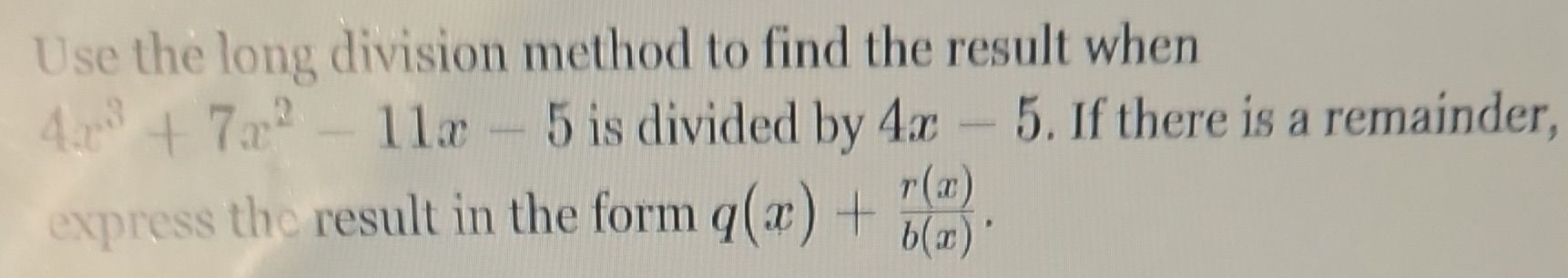
Use the long division method to find the result when 4x^(3)+7x^(2)-11 x-5 is divided by 4x-5. If there is a remainder, express the result in the form q(x)+(r(x))/(b(x)).

Question

Use the long division method to find the result when  4x^(3)+7x^(2)-11 x-5 is divided by  4x-5. If there is a remainder, express the result in the form  q(x)+(r(x))/(b(x)).

Bytelearn · Accepted Answer

Set up division: Set up the long division by writing $4x^3 + 7x^2 - 11x - 5$ under the long division symbol and $4x - 5$ outside.Find first quotient term: Divide the first term of the dividend, $4x^3$, by the first term of the divisor, $4x$, to get the first term of the quotient, $x^2$. Calculation: $4x^3 \div 4x = x^2$Multiply and subtract: Multiply the entire divisor $4x - 5$ by the first term of the quotient $x^2$ and write the result under the dividend. Calculation: $x^2 \cdot (4x - 5) = 4x^3 - 5x^2$Bring down next term: Subtract the result of the multiplication from the dividend to find the new dividend. Calculation: $(4x^3 + 7x^2) - (4x^3 - 5x^2) = 7x^2 - (-5x^2) = 7x^2 + 5x^2 = 12x^2$Find next quotient term: Bring down the next term of the original dividend, which is $-11x$, to get $12x^2 - 11x$.Multiply and subtract: Divide the first term of the new dividend, $12x^2$, by the first term of the divisor, $4x$, to get the next term of the quotient, $3x$. Calculation: $12x^2 \div 4x = 3x$Bring down next term: Multiply the entire divisor $4x - 5$ by the new term of the quotient $3x$ and write the result under the new dividend. Calculation: $3x \cdot (4x - 5) = 12x^2 - 15x$Find final quotient term: Subtract the result of the multiplication from the new dividend to find the next new dividend. Calculation: $(12x^2 - 11x) - (12x^2 - 15x) = 12x^2 - 12x^2 - 11x + 15x = 4x$Multiply and subtract: Bring down the next term of the original dividend, which is $-5$, to get $4x - 5$.Check for remainder: Divide the first term of the next new dividend, $4x$, by the first term of the divisor, $4x$, to get the next term of the quotient, $1$. Calculation: $4x \div 4x = 1$Multiply the entire divisor $4x - 5$ by the new term of the quotient $1$ and write the result under the next new dividend. Calculation: $1 \cdot (4x - 5) = 4x - 5$Subtract the result of the multiplication from the next new dividend to find the remainder. Calculation: $(4x - 5) - (4x - 5) = 4x - 4x - 5 + 5 = 0$Since the remainder is $0$, the division is exact and there is no remainder term to include in the final answer.

Use the long division method to find the result when $4 x^{3}+7 x^{2}-11 x-5$ is divided by $4 x-5$ . If there is a remainder, express the result in the form $q(x)+\frac{r(x)}{b(x)}$ .

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Use the long division method to find the result when 4x3+7x2−11x−5 4 x^{3}+7 x^{2}-11 x-5 4x3+7x2−11x−5 is divided by 4x−5 4 x-5 4x−5. If there is a remainder, express the result in the form q(x)+r(x)b(x) q(x)+\frac{r(x)}{b(x)} q(x)+b(x)r(x)​.

Use the long division method to find the result when $4 x^{3}+7 x^{2}-11 x-5$ is divided by $4 x-5$ . If there is a remainder, express the result in the form $q(x)+\frac{r(x)}{b(x)}$ .