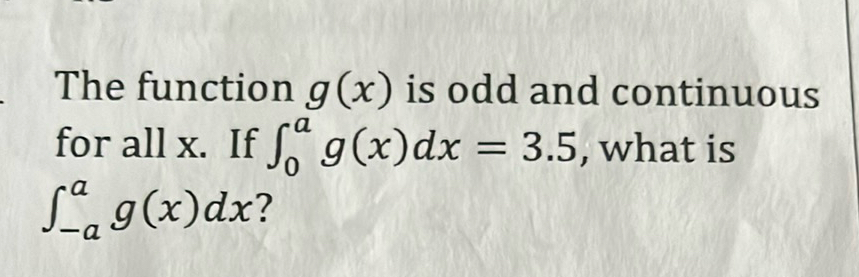Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The function g(x) is odd and continuous for all x. If int_(0)^(a)g(x)dx=3.5, what is int_(-a)^(a)g(x)dx?

The function g(x) g(x) is odd and continuous for all x \mathrm{x} . If ∫0ag(x)dx=3.5 \int_{0}^{a} g(x) d x=3.5 , what is ∫−aag(x)dx? \int_{-a}^{a} g(x) d x ?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

Q. The function g(x) g(x) is odd and continuous for all x \mathrm{x} . If ∫0ag(x)dx=3.5 \int_{0}^{a} g(x) d x=3.5 , what is ∫−aag(x)dx? \int_{-a}^{a} g(x) d x ?
  1. Identify Odd Function: Since g(x)g(x) is an odd function, the integral of g(x)g(x) from −a-a to 00 is the negative of the integral from 00 to aa.
  2. Calculate Integral from −a-a to 00: Calculate the integral of g(x)g(x) from −a-a to 00, which is −3.5-3.5 because the integral from 00 to aa is 3.53.5.
  3. Find Integral from −a-a to aa: Add the integral from −a-a to 00 and from 00 to aa to find the integral from −a-a to aa. So, −3.5+3.5=0-3.5 + 3.5 = 0.

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

View all (140)