Full solution
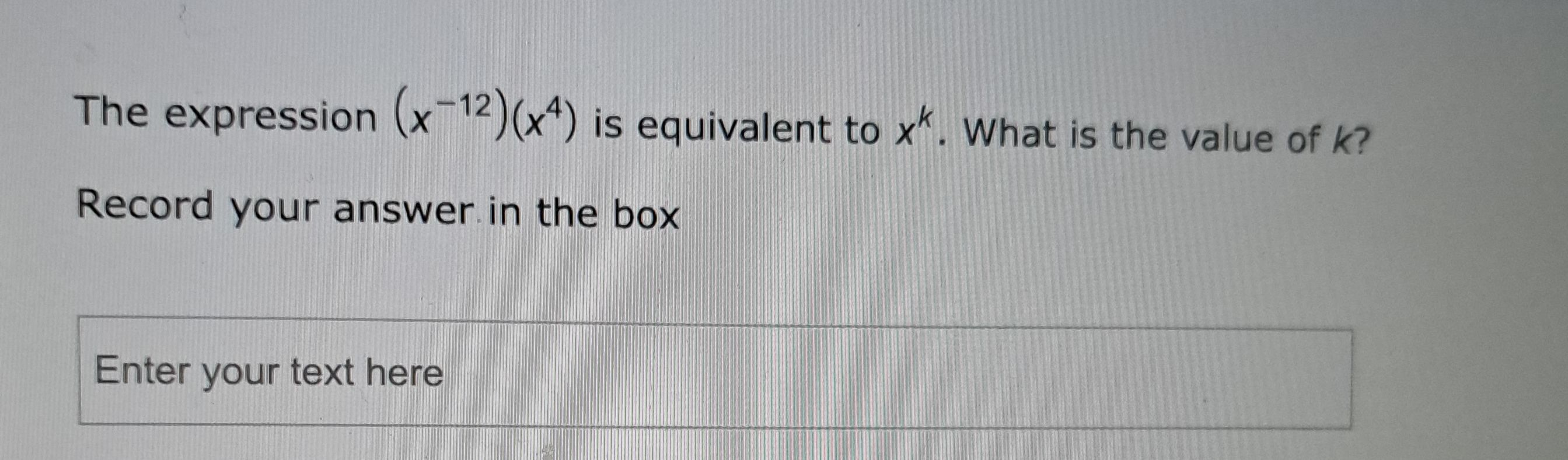
Q. The expression is equivalent to . What is the value of ?
- Identify Exponents: We are given the expression and we need to find the equivalent expression in the form of . According to the laws of exponents, when we multiply two expressions with the same base, we add their exponents.Calculation:
- Calculate Value of k: Perform the addition to find the value of k.Calculation:
- Find Equivalent Expression: We have found the value of to be . This means that the expression is equivalent to .