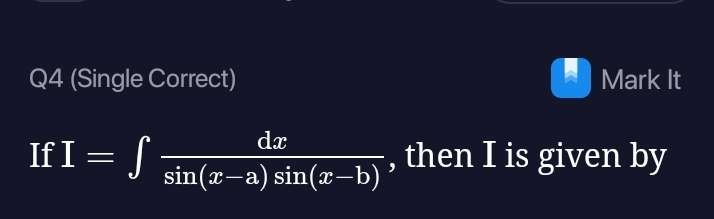If I=int(dx)/(sin(x-a)sin(x-b)), then I is given by

Question

If  I=int(dx)/(sin(x-a)sin(x-b)), then  I is given by

Bytelearn · Accepted Answer

Apply Trigonometric Identity: Let's use the identity sin(c)sin(d) = 1/2[cos(c-d) - cos(c+d)] to simplify the integral. So, sin(x-a)sin(x-b) = 1/2[cos((x-a)-(x-b)) - cos((x-a)+(x-b))].Simplify the Integral: This simplifies to 1/2[cos(b-a) - cos(2x-a-b)]. Now, I = int(dx)/(1/2[cos(b-a) - cos(2x-a-b)]).Factor Out Constants: We can take out the constant term 1/2 and cos(b-a) from the denominator, so I = 2int(dx)/[cos(b-a) - cos(2x-a-b)].Use Substitution: Now, let's use the substitution u = 2x - a - b, which means du = 2dx. So, dx = du/2.Integrate with Substitution: Substitute back into the integral, we get I = 2int(du/2)/[cos(b-a) - cos(u)]. This simplifies to I = int(du)/[cos(b-a) - cos(u)].Split Integral: Now, we can split the integral into two parts: I = int(du/cos(b-a)) - int(du/cos(u)).Evaluate First Integral: The first integral int(du/cos(b-a)) is just u/cos(b-a) since cos(b-a) is a constant.Evaluate Second Integral: The second integral int(du/cos(u)) is a standard integral that equals ln|sec(u) + tan(u)|.Combine Results: So, I = u/cos(b-a) - ln|sec(u) + tan(u)| + C, where C is the constant of integration.Substitute Back and Simplify: Now, substitute back u = 2x - a - b to get I in terms of x. I = (2x - a - b)/cos(b-a) - ln|sec(2x - a - b) + tan(2x - a - b)| + C.

If $I=\int \frac{\mathrm{d}x}{\sin(x-a)\sin(x-b)}$ , then $\newline$ $I$ is given by

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

If I=∫dxsin⁡(x−a)sin⁡(x−b)I=\int \frac{\mathrm{d}x}{\sin(x-a)\sin(x-b)}I=∫sin(x−a)sin(x−b)dx​, then \newlineIII is given by

If $I=\int \frac{\mathrm{d}x}{\sin(x-a)\sin(x-b)}$ , then $\newline$ $I$ is given by