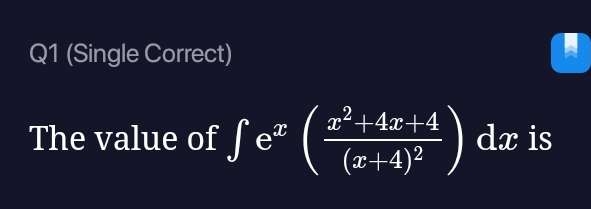The value of inte^(x)((x^(2)+4x+4)/((x+4)^(2)))dx is

Question

The value of  inte^(x)((x^(2)+4x+4)/((x+4)^(2)))dx is

Bytelearn · Accepted Answer

Simplify the integrand: Let's simplify the integrand first. Notice that (x^2 + 4x + 4) is the expansion of (x + 2)^2. So, we rewrite the integral as int(e^(x)((x+2)^2)/((x+4)^2))dx.Perform substitution: Now, let's do a substitution. Let u = x + 4, then du = dx and x = u - 4. Substitute into the integral to get int(e^(u-4)((u-2)^2)/(u^2))du.Expand the numerator: Expand the numerator to get int(e^(u-4)(u^2 - 4u + 4)/u^2)du.Split the integral: Split the integral into three parts: int(e^(u-4)du) - 4int(e^(u-4)/u)du + 4int(e^(u-4)/u^2)du.Calculate the first integral: The first integral int(e^(u-4)du) is straightforward, it's e^(u-4)/e^(-4) + C1, which simplifies to e^u/e^4 + C1.Calculate the second integral: The second integral -4int(e^(u-4)/u)du is a bit tricky, but we can use integration by parts or look it up as a standard integral. It's -4e^(-4)Ei(u) + C2, where Ei is the exponential integral.Calculate the third integral: The third integral 4int(e^(u-4)/u^2)du is also not standard, but we can use integration by parts. Let's set v = 1/u, dv = -1/u^2 du, and dw = e^(u-4)du, w = e^(u-4)/e^(-4). Then we get 4int(vdw) = 4vw - 4int(wdv).After calculating, we get 4(e^(u-4)/u)/e^4 - 4int(-e^(u-4)/u^2)du, which simplifies to 4e^u/(e^4u) - 4int(e^(u-4)/u^2)du.

$\newline$ The value of $\newline$ $\int e^{x}\left(\frac{x^{2}+4x+4}{(x+4)^{2}}\right)dx$ is

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

\newlineThe value of \newline∫ex(x2+4x+4(x+4)2)dx\int e^{x}\left(\frac{x^{2}+4x+4}{(x+4)^{2}}\right)dx∫ex((x+4)2x2+4x+4​)dx is

$\newline$ The value of $\newline$ $\int e^{x}\left(\frac{x^{2}+4x+4}{(x+4)^{2}}\right)dx$ is