Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

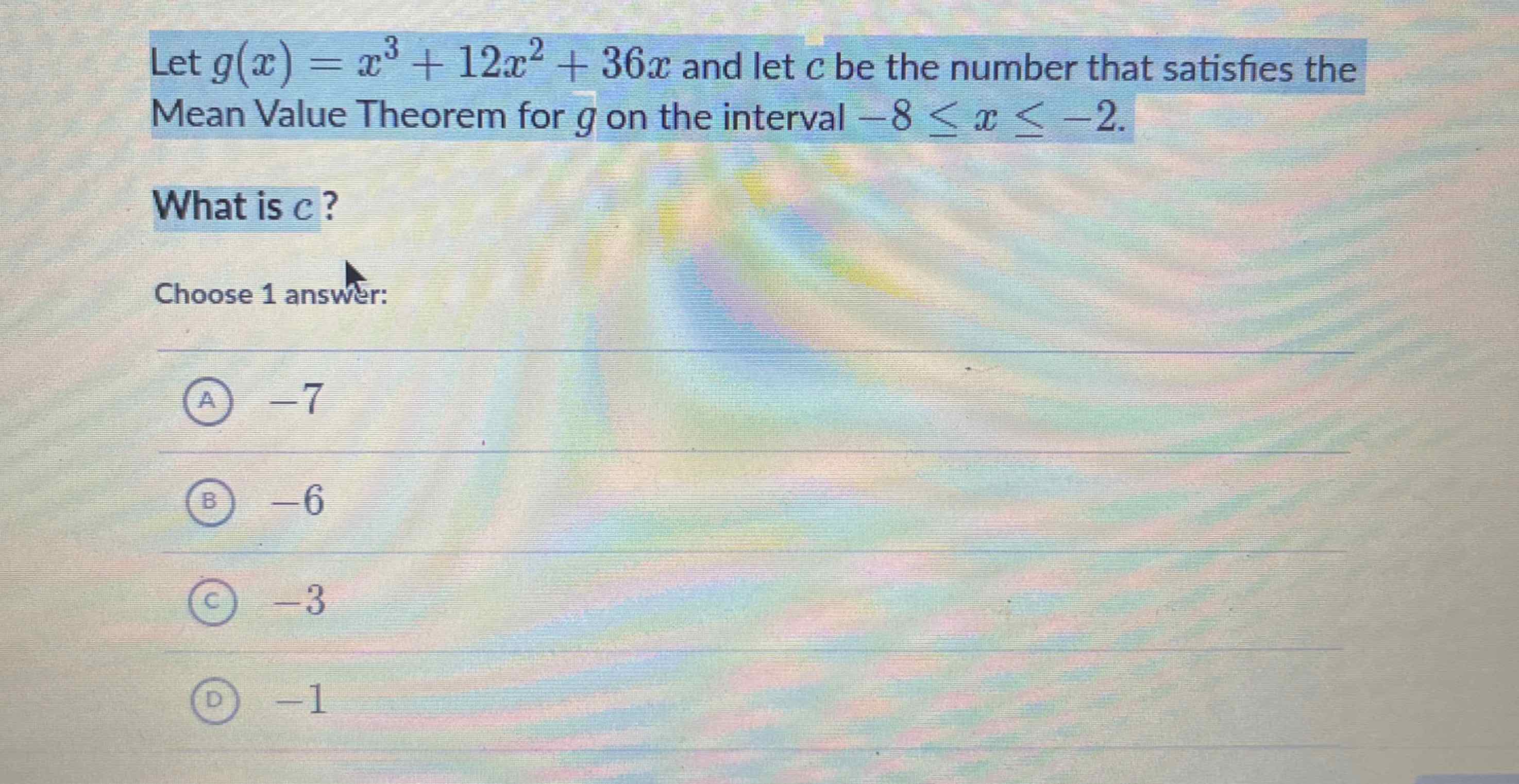
Let
g(x)=x^(3)+12x^(2)+36 x and let
c be the number that satisfies the Mean Value Theorem for
g on the interval
-8 <= x <= -2.
What is
c ?
Choose 1 answer:
(A) -7
(B) -6
(c) -3
(b) -1

Let $g(x)=x^{3}+12x^{2}+36x$ and let $c$ be the number that satisfies the Mean Value Theorem for $g$ on the interval $-8 \leq x \leq -2$ . $\newline$ What is $c$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-7$ $\newline$ (B) $-6$ $\newline$ (C) $-3$ $\newline$ (D) $-1$

View step-by-step help

View step-by-step help

Full solution

Q. Let

g(x)=x^{3}+12x^{2}+36x

and let

c

be the number that satisfies the Mean Value Theorem for

g

on the interval

-8 \leq x \leq -2

.

\newline

What is

c

?

\newline

Choose

1

answer:

\newline

(A)

-7

\newline

(B)

-6

\newline

(C)

-3

\newline

(D)

-1

Calculate Derivative of $g(x)$ : Calculate the derivative of $g(x)$ to apply the Mean Value Theorem. $\newline$ $g(x) = x^3 + 12x^2 + 36x$ $\newline$ $g'(x) = 3x^2 + 24x + 36$
Apply Mean Value Theorem: Apply the Mean Value Theorem, which states there exists a $c$ in $(-8, -2)$ such that $g'(-8) = g'(-2)$ . $\newline$ Calculate $g'(-8)$ and $g'(-2)$ : $\newline$ $g'(-8) = 3(-8)^2 + 24(-8) + 36 = 192 - 192 + 36 = 36$ $\newline$ $g'(-2) = 3(-2)^2 + 24(-2) + 36 = 12 - 48 + 36 = 0$
Find $c$ for $g'(-8) = g'(-2)$ : Find $c$ such that $g'(-8) = g'(-2)$ . $\newline$ Since $g'(-8) \neq g'(-2)$ , there's a mistake in the calculation of $g'(-2)$ . $\newline$ Recalculate $g'(-2)$ : $\newline$ $g'(-2) = 3(-2)^2 + 24(-2) + 36 = 12 - 48 + 36 = 0$

More problems from Euler's method

Question

f(x)=x^{3}-6 x^{2}+12 x

c

be the number that satisfies the Mean Value Theorem for

f

on the interval

[0,3]

\newline

c

\newline

1

\newline

0

\newline

1

\newline

2

\newline

3

Posted 8 months ago

Question

g(x)=x^{3}+12 x^{2}+36 x

c

be the number that satisfies the Mean Value Theorem for

g

on the interval

-8 \leq x \leq-2

\newline

c

\newline

1

\newline

-7

\newline

-6

\newline

-3

\newline

-1

Posted 8 months ago

Question

h(x)=x^{3}-6 x^{2}-10 x

c

be the number that satisfies the Mean Value Theorem for

h

on the interval

[-4,5]

\newline

c

\newline

1

\newline

-2

\newline

-1

\newline

1

\newline

3

Posted 8 months ago

Question

g(x)=2 x^{3}-21 x^{2}+60 x

\newline

What is the absolute maximum value of

g

over the closed interval

[0,6]

\newline

1

\newline

25

\newline

42

\newline

36

\newline

52

Posted 7 months ago

Question

f(x)=2 x^{3}+21 x^{2}+36 x

\newline

What is the absolute maximum value of

f

over the closed interval

[-8,0]

\newline

1

\newline

32

\newline

\mathbf{1 8 0}

\newline

\mathbf{1 0 8}

\newline

0

Posted 8 months ago

Question

h(x)=x^{3}+6 x^{2}+2

\newline

What is the absolute minimum value of

h

over the closed interval

-6 \leq x \leq 2

\newline

1

\newline

34

\newline

-34

\newline

2

\newline

-2

Posted 8 months ago

Question

1,000=20z^{2}

\newline

How many distinct real solutions does the given equation have?

\newline

1

\newline

0

\newline

1

\newline

2

\newline

4

Posted 8 months ago

Question

Dante commutes to work

4

mornings a week. For his commute each morning, he walks for

10

minutes, waits and rides the bus for

x

minutes, and waits and rides the train for

y

minutes. If Dante spends at least

3.5

hours on his morning commute each week, which of the following inequalities best describes Dante's weekly morning commute?

\newline

1

\newline

x+y+10 \geq 3.5(60)

\newline

x+y+10 \geq 3.5(60)(4)

\newline

4(x+y)+10 \geq 3.5(60)

\newline

4(x+y+10) \geq 3.5(60)

Posted 8 months ago

Question

\frac{1}{3}x+3y=4

\newline

2x-4=2y

\newline

Consider the given system of equations. If

(x,y)

is the solution to the system, then what is the value of

x-y

\newline

\square

Posted 8 months ago

Question

Which of the following is the derivative

\frac{d y}{d x}

for the plane curve defined by the equations

x(t)=\frac{1}{2} \sin 2 t

y(t)=2 \cos 2 t

0 \leq t \leq 2 \pi

\newline

Select the correct answer below:

\newline

4 \cot 2 t

\newline

\tan 4 t

\newline

-\tan 4 t

\newline

-4 \tan 2 t

Posted 6 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant