Full solution
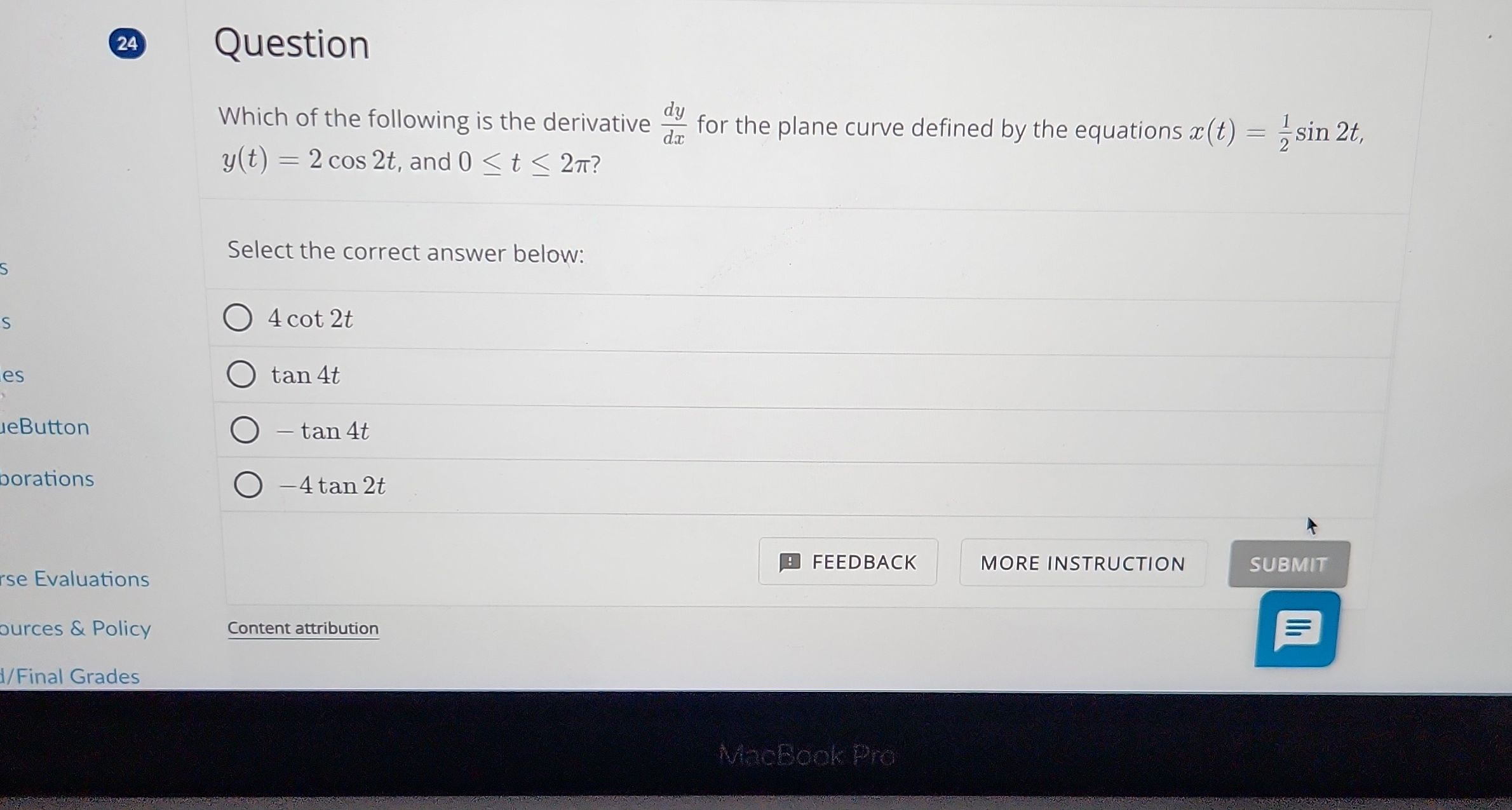
Q. Which of the following is the derivative for the plane curve defined by the equations , , and ?Select the correct answer below:(A) (B) (C) (D)
- Find Derivative Process: To find the derivative , we need to find and first and then divide by .
- Calculate : Calculate :
- Calculate : Calculate :
- Find by dividing by (\frac{dy}{dx}) = \frac{(\frac{dy}{dt})}{(\frac{dx}{dt})} = \frac{(\(4\)\sin(\(2\)t))}{(\cos(\(2\)t))} = \(4\tan(t)
- Check Answer Choices: However, we need to check the answer choices to see which one matches our result. The correct answer should be in terms of and should match the form of the derivative we found.
- Correcting Mistake: The answer choices are:A) B) C) D) Our result is , which is not listed. We need to check if we made a mistake or if there is a trigonometric identity that can transform our result into one of the given options.
- Correcting Mistake: The answer choices are:A) B) C) D) Our result is , which is not listed. We need to check if we made a mistake or if there is a trigonometric identity that can transform our result into one of the given options.Upon reviewing, we realize that we made a mistake in our calculation. The correct derivative should be in terms of , not . Therefore, the correct answer should be because the derivative of with respect to is negative, and we missed the negative sign in our previous step.
More problems from Euler's method
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help