Let g(x)=x^(3)+12x^(2)+36 x and let c be the number that satisfies the Mean Value Theorem for g on the interval -8

Question

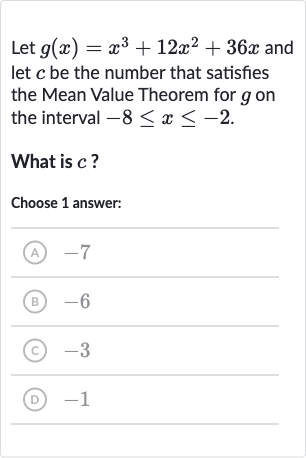
Let  g(x)=x^(3)+12x^(2)+36 x and let  c be the number that satisfies the Mean Value Theorem for  g on the interval  -8 <= x <= -2. What is  c ? Choose 1 answer: (A) -7 (B) -6 (C) -3 (D) -1

Bytelearn · Accepted Answer

Mean Value Theorem Explanation: The Mean Value Theorem states that if a function g is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one number c in the interval (a, b) such that g'(c) is equal to the average rate of change of the function over [a, b]. The average rate of change is given by (g(b) - g(a)) / (b - a).Calculate g(-2) and g(-8): First, we need to find g(-2) and g(-8) to calculate the average rate of change of g(x) on the interval [-8, -2]. g(-2) = (-2)^3 + 12(-2)^2 + 36(-2) = -8 + 48 - 72 = -32 g(-8) = (-8)^3 + 12(-8)^2 + 36(-8) = -512 + 768 - 288 = -32Calculate Average Rate of Change: Now, we calculate the average rate of change of g(x) on the interval [-8, -2]. Average rate of change = (g(-2) - g(-8)) / (-2 - (-8)) = (-32 - (-32)) / (6) = 0 / 6 = 0Find Derivative g'(x): Next, we need to find g'(x), the derivative of g(x), to find the value of c that satisfies g'(c) = average rate of change. g'(x) = d/dx [x^3 + 12x^2 + 36x] = 3x^2 + 24x + 36Solve for c: We set g'(c) equal to the average rate of change and solve for c. 0 = g'(c) = 3c^2 + 24c + 36 This is a quadratic equation in the form of 3c^2 + 24c + 36 = 0.Quadratic Equation Solution: We can solve the quadratic equation by factoring or using the quadratic formula. Since the equation is already factored as 3(c^2 + 8c + 12) = 0, we can factor further to find the roots. 3(c + 6)(c + 2) = 0Final Value of c: Setting each factor equal to zero gives us the potential values for c. c + 6 = 0 or c + 2 = 0 c = -6 or c = -2However, c must be in the open interval (-8, -2), so c cannot be -2. Therefore, the only value that satisfies the Mean Value Theorem in the given interval is c = -6.

Let $g(x)=x^{3}+12 x^{2}+36 x$ and let $c$ be the number that satisfies the Mean Value Theorem for $g$ on the interval $-8 \leq x \leq-2$ . $\newline$ What is $c$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-7$ $\newline$ (B) $-6$ $\newline$ (C) $-3$ $\newline$ (D) $-1$

Full solution

More problems from Euler's method

Related topics