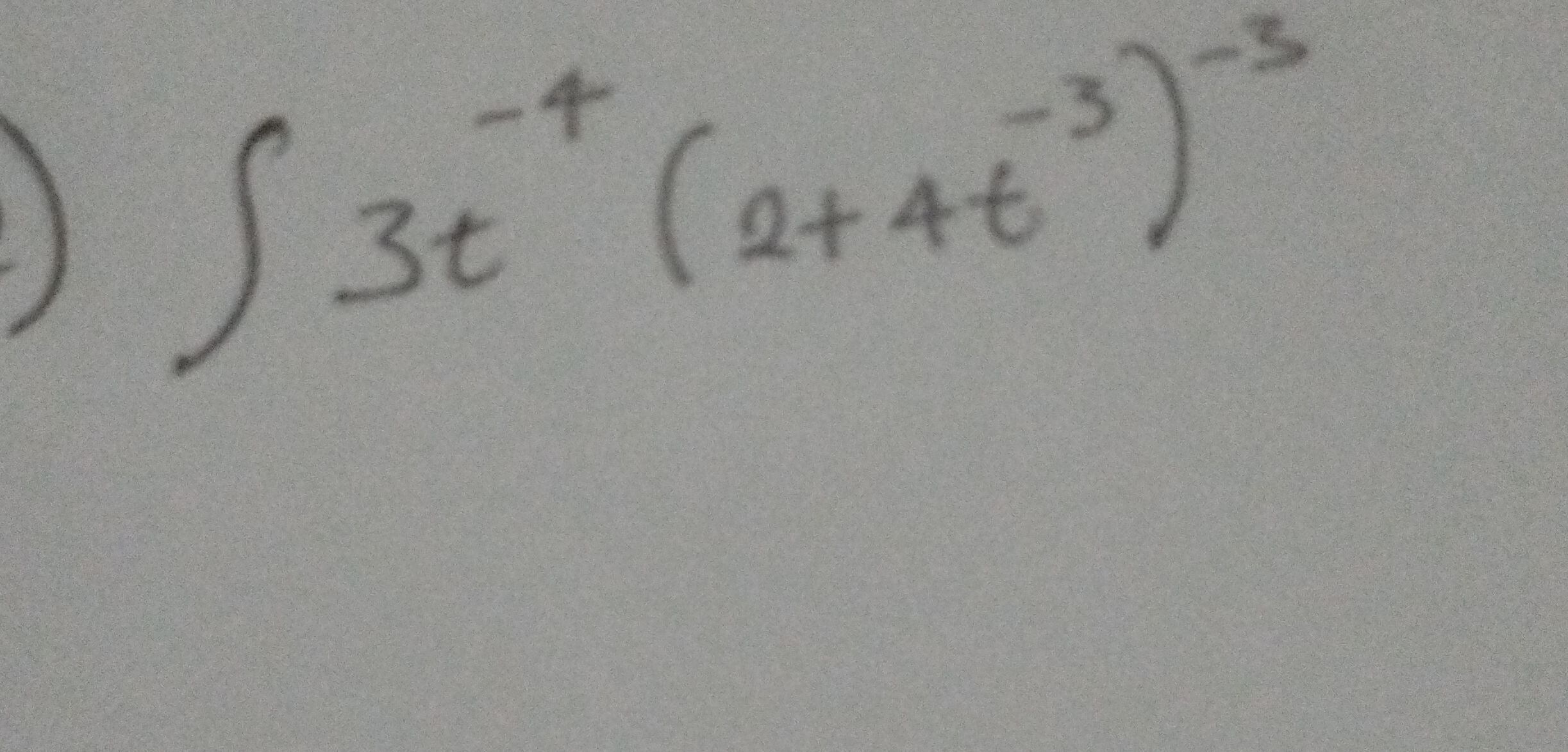Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int3t^(-4)(2+4t^(-3))^(-3)

∫3t−4(2+4t−3)−3 \int 3 t^{-4}\left(2+4 t^{-3}\right)^{-3}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Gaussian integralright chevron icon

Full solution

Q. ∫3t−4(2+4t−3)−3 \int 3 t^{-4}\left(2+4 t^{-3}\right)^{-3}
  1. Identify inner function: Given the integral to solve:\newlineI=∫3t−4(2+4t−3)−3 dtI = \int 3t^{-4}(2+4t^{-3})^{-3} \, dt\newlineIdentify the inner function for substitution.\newlineLet u=2+4t−3u = 2 + 4t^{-3}
  2. Differentiate uu: Differentiate uu with respect to tt to find dudt\frac{du}{dt}.dudt=ddt(2+4t−3)=0−12t−4=−12t−4\frac{du}{dt} = \frac{d}{dt} (2 + 4t^{-3}) = 0 - 12t^{-4} = -12t^{-4}
  3. Solve for dtdt: Solve for dtdt in terms of dudu and tt.dt=du(−12t−4)dt = \frac{du}{(-12t^{-4})}
  4. Substitute uu and dtdt: Substitute uu and dtdt into the integral.\newlineI=∫3t−4(u)−3∗(du−12t−4)I = \int 3t^{-4}(u)^{-3} * (\frac{du}{-12t^{-4}})\newline =∫−14∗u−3du= \int -\frac{1}{4} * u^{-3} du
  5. Integrate with respect: Integrate with respect to uu.
    I=−14∫u−3 duI = -\frac{1}{4} \int u^{-3} \, du
    =−14⋅(−12)⋅u−2= -\frac{1}{4} \cdot (-\frac{1}{2}) \cdot u^{-2}
    =18⋅u−2= \frac{1}{8} \cdot u^{-2}
  6. Substitute back for u: Substitute back for u to get the integral in terms of tt.I=18×(2+4t−3)−2I = \frac{1}{8} \times \left(2 + 4t^{-3}\right)^{-2}
  7. Add constant of integration: Add the constant of integration CC to the result.I=18⋅(2+4t−3)−2+CI = \frac{1}{8} \cdot (2 + 4t^{-3})^{-2} + C

More problems from Gaussian integral

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

View all (20)