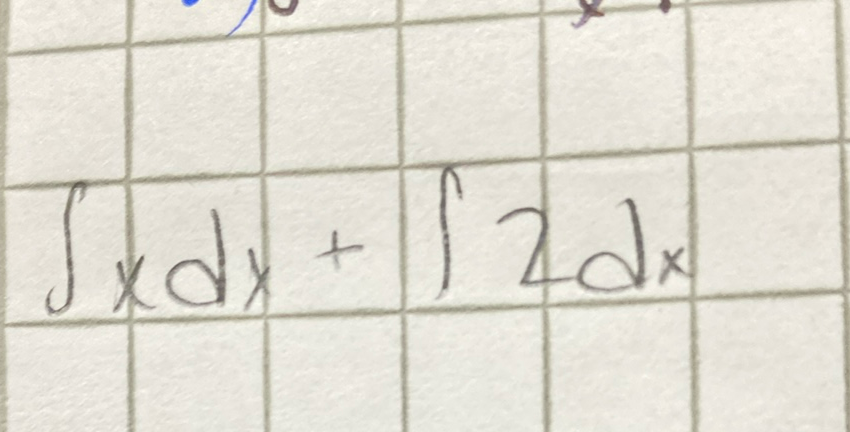Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int xdx+int2dx

$\int x d x+\int 2 d x$

View step-by-step help

View step-by-step help

Find indefinite integrals using the substitution and by parts

Full solution

Q.

\int x d x+\int 2 d x

Separate into Two Integrals: We are given the integral of a sum of two functions, which can be separated into two integrals. The integral of $x$ with respect to $x$ , and the integral of $2$ with respect to $x$ . We can use the linearity of the integral to separate them. $\newline$ Calculation: $\int(x \, dx) + \int(2 \, dx)$
Integrate $x$ with Power Rule: To integrate $x$ with respect to $x$ , we use the power rule for integration. The power rule states that $\int x^n \, dx = \frac{x^{(n+1)}}{n+1} + C$ , where $n \neq -1$ . In our case, $n = 1$ . $\newline$ Calculation: $\int x \, dx = \frac{x^{(1+1)}}{1+1} + C = \frac{x^2}{2} + C$
Integrate Constant $2$ : To integrate the constant $2$ with respect to $x$ , we use the fact that the integral of a constant $a$ with respect to $x$ is $ax + C$ .
Calculation: $\int 2 \, dx = 2x + C$
Combine Results for Final Answer: Now we combine the results of the two integrals to get the final answer. $\newline$ Calculation: $(\frac{x^2}{2} + 2x + C)$

More problems from Find indefinite integrals using the substitution and by parts

Question

Evaluate the integral.

\newline

\int-x 4^{-3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{3} e^{-2 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int x 5^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-2 x e^{2 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-2 x \cos (-2 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-x \cos (-3 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 5^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-6 x 4^{-4 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 2^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-3 x \sin (-2 x) d x

\newline

Posted 2 months ago