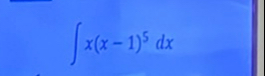Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int x(x-1)^(5)dx

$\int x(x-1)^{5} d x$

View step-by-step help

View step-by-step help

Find indefinite integrals using the substitution and by parts

Full solution

Q.

\int x(x-1)^{5} d x

Recognize opportunity for integration by parts: Recognize the integral as an opportunity to use integration by parts. Integration by parts formula: $\int u \, dv = uv - \int v \, du$ Let $u = x$ and $dv = (x-1)^5 \, dx$ .
Differentiate $u$ and integrate $dv$ : Differentiate $u$ and integrate $dv$ . $du = dx$ and $v = \int(x-1)^5 dx$ . To find $v$ , we need to integrate $(x-1)^5$ .
Integrate $(x-1)^5$ using substitution: Integrate $(x-1)^5$ using the substitution method. $\newline$ Let $t = x - 1$ , then $dt = dx$ and when $x = 1$ , $t = 0$ . $\newline$ Now we integrate $t^5 dt$ .
Calculate integral of $t^5$ : Calculate the integral of $t^5$ . $\int t^5 \, dt = \left(\frac{1}{6}\right)t^6 + C$ Now we substitute back $x - 1$ for $t$ . $v = \left(\frac{1}{6}\right)(x - 1)^6 + C$
Apply integration by parts formula: Apply the integration by parts formula. $\newline$ $\int x(x-1)^5 \, dx = uv - \int v \, du$ $\newline$ = $x \cdot \left[\frac{1}{6}(x - 1)^6 + C\right] - \int\left[\frac{1}{6}(x - 1)^6 + C\right] \, dx$
Simplify expression and integrate remaining term: Simplify the expression and integrate the remaining term. $\newline$ $= \frac{1}{6}x(x - 1)^6 - \frac{1}{6}\int(x - 1)^6 dx$ $\newline$ Now we need to integrate $(x - 1)^6$ .
Integrate $(x - 1)^6$ using substitution: Integrate $(x - 1)^6$ using the substitution method. $\newline$ Let $t = x - 1$ , then $dt = dx$ and when $x = 1$ , $t = 0$ . $\newline$ Now we integrate $t^6 dt$ .
Calculate integral of $t^6$ : Calculate the integral of $t^6$ . $\int t^6 \, dt = \left(\frac{1}{7}\right)t^7 + C$ Now we substitute back $x - 1$ for $t$ . $\int(x - 1)^6 \, dx = \left(\frac{1}{7}\right)(x - 1)^7 + C$
Substitute integral back into expression: Substitute the integral back into the expression. $\newline$ $= \frac{1}{6}x(x - 1)^6 - \frac{1}{6} \times \left[\frac{1}{7}(x - 1)^7 + C\right]$ $\newline$ $= \frac{1}{6}x(x - 1)^6 - \frac{1}{42}(x - 1)^7 - \frac{C}{6}$
Combine constants and write final answer: Combine the constants and write the final answer. $\newline$ The indefinite integral of $x(x-1)^5$ with respect to $x$ is: $\newline$ $I = \frac{1}{6}x(x - 1)^6 - \frac{1}{42}(x - 1)^7 + C$ $\newline$ Where $C$ is the constant of integration.

More problems from Find indefinite integrals using the substitution and by parts

Question

Evaluate the integral.

\newline

\int-x 4^{-3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{3} e^{-2 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int x 5^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-2 x e^{2 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-2 x \cos (-2 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-x \cos (-3 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 5^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-6 x 4^{-4 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 2^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-3 x \sin (-2 x) d x

\newline

Posted 2 months ago