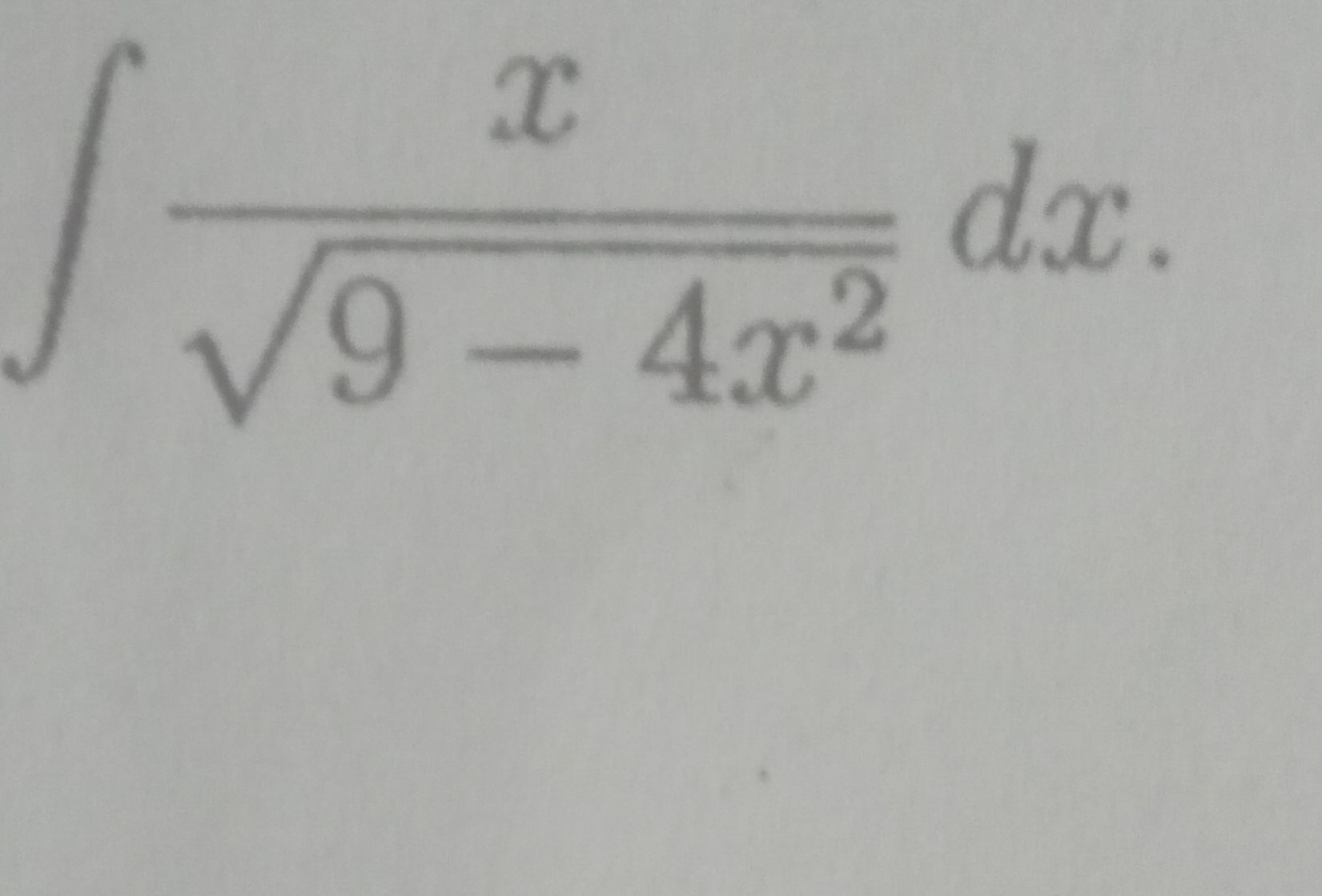AI tutor
Full solution
Q.
- Identify Integral: Identify the integral to be solved.We need to find the indefinite integral of the function .
- Trigonometric Substitution: Use a trigonometric substitution to simplify the integral.Let , which implies . Then, .
- Substitute Trigonometric Expressions: Substitute and in the integral with the trigonometric expressions.
- Simplify Integral: Simplify the integral.Since is always positive for in the range , which corresponds to the range of , we can remove the absolute value.
- Integrate with Respect: Integrate with respect to ., where is the constant of integration.
- Substitute Back Variable: Substitute back the original variable .Since , we have . To find , we use the Pythagorean identity ..
- Replace Cosine in Integral: Replace in the integral result.