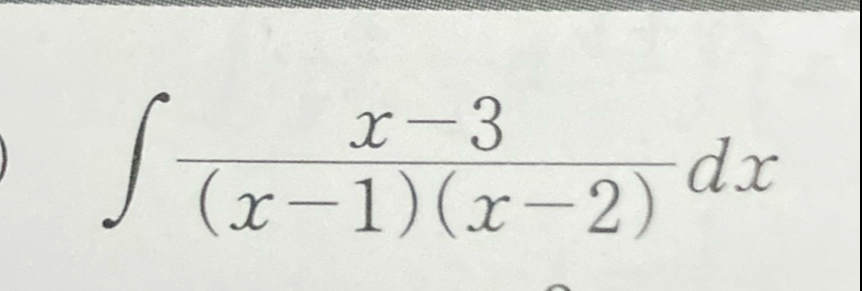AI tutor
Full solution
Q.
- Set up decomposition: We need to integrate the function . To do this, we will use partial fractions" target="_blank" class="backlink">fraction decomposition to express the integrand as a sum of simpler fractions that we can integrate individually.
- Find and : First, we set up the partial fraction decomposition:We need to find the values of and .
- Plug in x values: To find and , we multiply both sides of the equation by to get rid of the denominators:
- Calculate integrals: Now we will find the values of and by plugging in convenient values for . Let's first plug in :
- Integrate : Next, we plug in :
- Integrate : Now that we have and , we rewrite the original integral:\int\frac{x\(-3\)}{(x\(-1\))(x\(-2\))}dx = \int\left(\frac{\(2\)}{x\(-1\)} - \frac{\(1\)}{x\(-2\)}\right)dx
- Combine results: We can now integrate each term separately: \(\int\left(\frac{\(2\)}{x\(-1\)}\right)dx - \int\left(\frac{\(1\)}{x\(-2\)}\right)dx
- Final indefinite integral: The integral of \(\frac{2}{x-1} is , and the integral of is . So we have:, where is the constant of integration.
- Final indefinite integral: The integral of is , and the integral of is . So we have:, where is the constant of integration.We have found the indefinite integral of the given function: