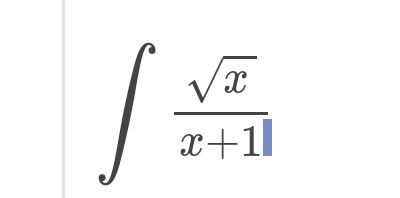int(sqrtx)/(x+1)

Question

int(sqrtx)/(x+1)

Bytelearn · Accepted Answer

Perform Substitution: Let I = ∫(sqrt(x))/(x+1) dx. To solve this integral, we will perform a substitution. Let u = x + 1, which implies that du = dx and x = u - 1.Rewrite in terms of u: Rewrite the integral in terms of u. The integral becomes I = ∫(sqrt(u - 1))/u du.Simplify Integral: This integral does not have a straightforward antiderivative, so we will try to simplify it further. We can split the integral into two parts using the property of integrals that ∫f(x) + g(x) dx = ∫f(x) dx + ∫g(x) dx. However, in this case, it does not seem to simplify the problem. We need to find another approach.Attempt Integration by Parts: Since the direct approach does not simplify the integral, we will try integration by parts. However, this also does not seem to lead to a simplification because we do not have a product of functions that would be suitable for integration by parts. We need to find a different method.Try Another Substitution: We will attempt a different substitution to simplify the integral. Let's try the substitution x = t^2, which implies that dx = 2t dt and sqrt(x) = t.Rewrite in terms of t: Rewrite the integral in terms of t. The integral becomes I = ∫t/(t^2 + 1) * 2t dt = 2∫t^2/(t^2 + 1) dt.Split Integral into Two Parts: Now we can split the integral into two parts: 2∫(t^2 + 1 - 1)/(t^2 + 1) dt = 2∫1 dt - 2∫1/(t^2 + 1) dt.Integrate Separately: Integrate both parts separately. The first part is straightforward: 2∫1 dt = 2t. The second part is a standard integral: 2∫1/(t^2 + 1) dt = 2arctan(t).Combine Results: Combine the results of the two integrals. I = 2t - 2arctan(t) + C, where C is the constant of integration.Substitute back for t: Substitute back for t to get the integral in terms of x. Since t = sqrt(x), we have I = 2sqrt(x) - 2arctan(sqrt(x)) + C.

$\int \frac{\sqrt{x}}{x+1}$

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

∫xx+1 \int \frac{\sqrt{x}}{x+1} ∫x+1x​​

$\int \frac{\sqrt{x}}{x+1}$