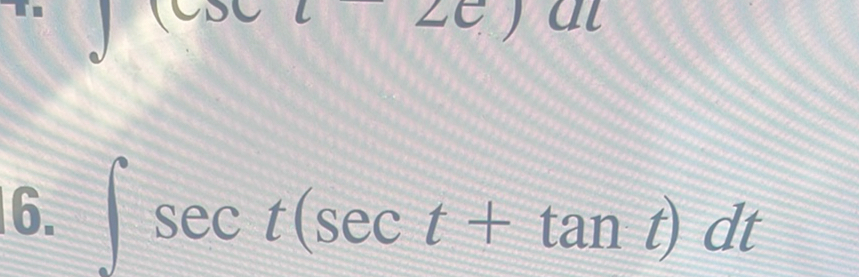Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int sec t(sec t+tan t)dt

∫sec⁡t(sec⁡t+tan⁡t)dt \int \sec t(\sec t+\tan t) d t =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitution and by partsright chevron icon

Full solution

Q. ∫sec⁡t(sec⁡t+tan⁡t)dt \int \sec t(\sec t+\tan t) d t =
  1. Distribute sec⁡(t)\sec(t): Rewrite the integral by distributing sec⁡(t)\sec(t) inside the parentheses.\newlineCalculation: \int \sec(t)(\sec(t) + \tan(t)) \, dt = \int (\sec^\(2(t) + \sec(t)\tan(t)) \, dt
  2. Integrate each term: Integrate each term separately.\newlineCalculation: ∫sec⁡2(t) dt+∫sec⁡(t)tan⁡(t) dt\int \sec^2(t) \, dt + \int \sec(t)\tan(t) \, dt
  3. Find integrals: The integral of sec⁡2(t)\sec^2(t) is tan⁡(t)\tan(t), and the integral of sec⁡(t)tan⁡(t)\sec(t)\tan(t) is sec⁡(t)\sec(t).\newlineCalculation: tan⁡(t)+sec⁡(t)+C\tan(t) + \sec(t) + C
  4. Combine results: Combine the results to get the final answer.\newlineCalculation: tan⁡(t)+sec⁡(t)+C\tan(t) + \sec(t) + C

More problems from Find indefinite integrals using the substitution and by parts

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

View all (140)