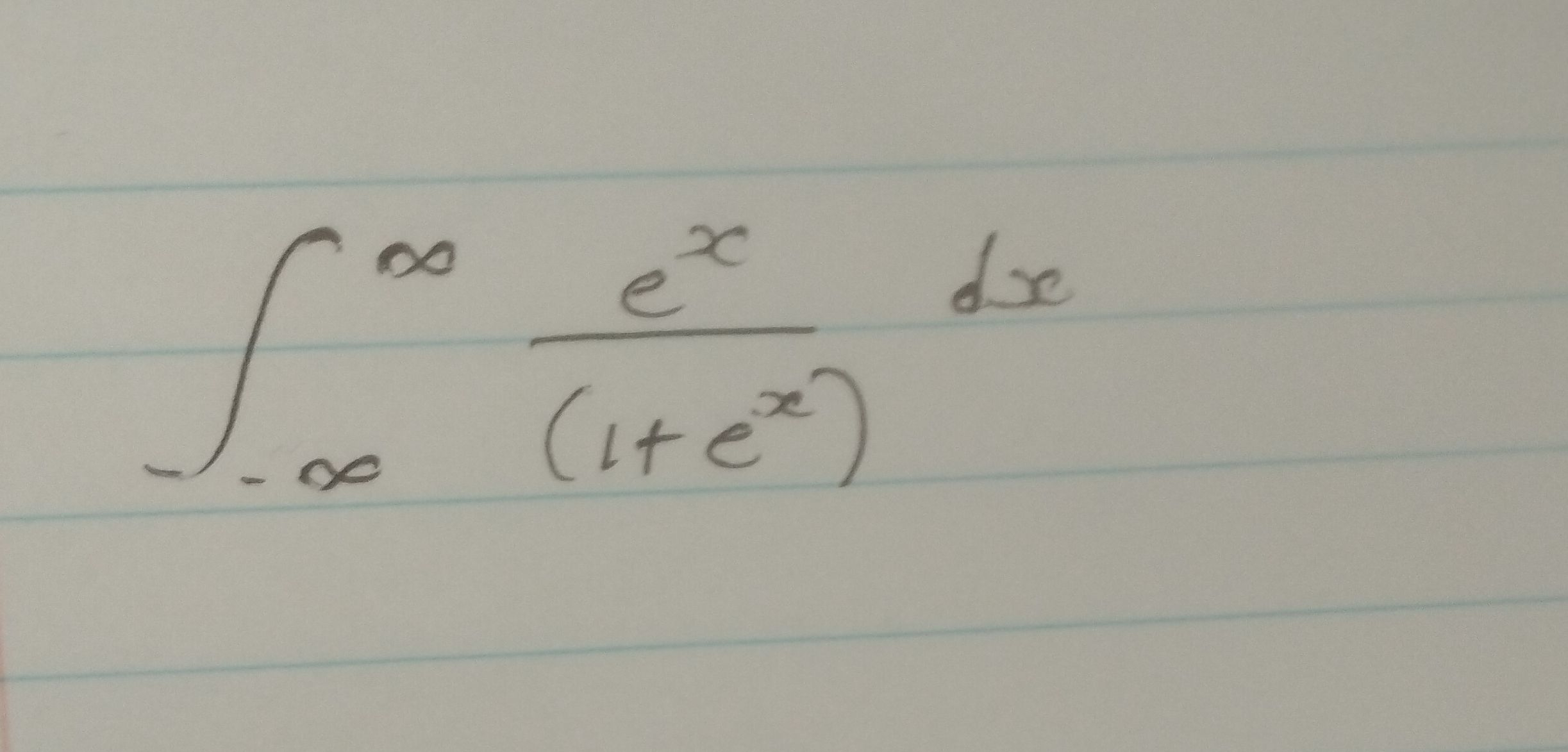Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int_(-oo)^(oo)(e^(x))/((1+e^(x)))dx

Evaluate the integral : ∫−∞∞ex(1+ex)dx \int_{-\infty}^{\infty} \frac{e^{x}}{\left(1+e^{x}\right)} d x

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Gaussian integralright chevron icon

Full solution

Q. Evaluate the integral : ∫−∞∞ex(1+ex)dx \int_{-\infty}^{\infty} \frac{e^{x}}{\left(1+e^{x}\right)} d x
  1. Substitution and Simplification: Simplify the integral using a substitution.\newlineLet u=exu = e^x, then du=exdxdu = e^x dx, or dx=duudx = \frac{du}{u}.\newlineSubstitute into the integral:\newline∫(−∞)(∞)ex(1+ex)dx=∫0∞1(1+u)⋅duu\int_{(-\infty)}^{(\infty)}\frac{e^{x}}{(1+e^{x})}dx = \int_{0}^{\infty}\frac{1}{(1+u)} \cdot \frac{du}{u}
  2. Evaluate Integral with New Variable: Evaluate the integral with the new variable.\newlineThe limits change as xx approaches −∞-\infty, uu approaches 00, and as xx approaches ∞\infty, uu approaches ∞\infty.\newlineSo, ∫0∞11+u⋅(duu)=∫0∞1u(1+u)du\int_{0}^{\infty}\frac{1}{1+u} \cdot \left(\frac{du}{u}\right) = \int_{0}^{\infty}\frac{1}{u(1+u)}du
  3. Decompose Fraction: Decompose the fraction.\newline1u(1+u)\frac{1}{u(1+u)} can be written as Au+B1+u\frac{A}{u} + \frac{B}{1+u}.\newlineSolving for AA and BB:\newline1=A(1+u)+Bu1 = A(1+u) + Bu\newlineSetting u=0u=0, A=1A = 1.\newlineSetting u=−1u=-1, B=−1B = -1 (which is incorrect, should be B=0B = 0).

More problems from Gaussian integral

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 2 months ago

View all (21)