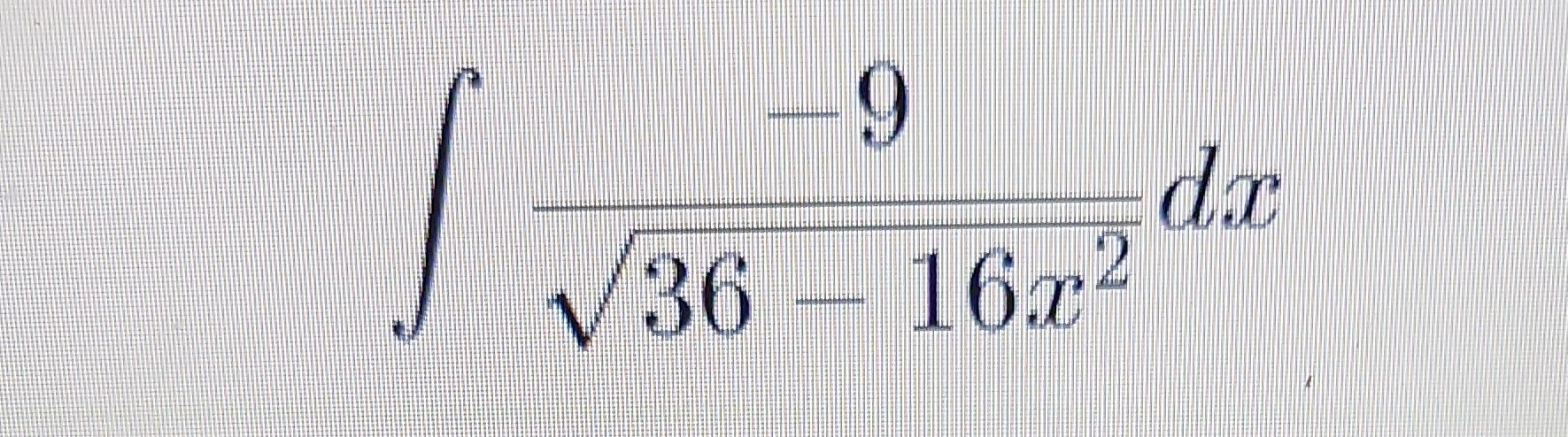Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral: int(-9)/(sqrt(36-16x^(2)))dx =

Evaluate the integral:∫−936−16x2dx \int \frac{-9}{\sqrt{36-16 x^{2}}} d x =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

Q. Evaluate the integral:∫−936−16x2dx \int \frac{-9}{\sqrt{36-16 x^{2}}} d x =
  1. Given Integral: We are given the integral: \newline∫−936−16x2dx\int \frac{-9}{\sqrt{36-16x^{2}}}dx\newlineTo solve this, we can recognize that this integral is in the form of an integral that results from a trigonometric substitution. Specifically, we can use the substitution x=34sin⁡(θ)x = \frac{3}{4}\sin(\theta) to simplify the square root term.
  2. Trigonometric Substitution: First, let's make the substitution x=34sin⁡(θ)x = \frac{3}{4}\sin(\theta). Then, dx=34cos⁡(θ)d(θ)dx = \frac{3}{4}\cos(\theta)d(\theta). We also need to express the square root in terms of θ\theta. Substituting xx into the square root gives us 36−16x2=36−16(34)2sin⁡2(θ)=36−9sin⁡2(θ)\sqrt{36 - 16x^2} = \sqrt{36 - 16\left(\frac{3}{4}\right)^2\sin^2(\theta)} = \sqrt{36 - 9\sin^2(\theta)}.
  3. Simplify Square Root: Now, we simplify the square root: 36−9sin⁡2(θ)=36(1−sin⁡2(θ))=36cos⁡2(θ)=6cos⁡(θ)\sqrt{36 - 9\sin^2(\theta)} = \sqrt{36(1 - \sin^2(\theta))} = \sqrt{36\cos^2(\theta)} = 6\cos(\theta). We can now substitute xx and dxdx into the integral and replace the square root with 6cos⁡(θ)6\cos(\theta).
  4. Substitute xx and dxdx: The integral becomes: ∫−96cos⁡(θ)⋅(34)cos⁡(θ)d(θ)=∫(−9⋅34)d(θ)=∫(−274)d(θ)\int\frac{-9}{6\cos(\theta)} \cdot \left(\frac{3}{4}\right)\cos(\theta)d(\theta) = \int\left(-9 \cdot \frac{3}{4}\right)d(\theta) = \int\left(-\frac{27}{4}\right)d(\theta)
  5. Integrate: Integrating −274-\frac{27}{4} with respect to θ\theta gives us:\newline−274⋅θ+C-\frac{27}{4} \cdot \theta + C
  6. Back-Substitute for xx: Now we need to back-substitute to get the answer in terms of xx. From our substitution x=34sin⁡(θ)x = \frac{3}{4}\sin(\theta), we can solve for θ\theta: θ=arcsin⁡(4x3)\theta = \arcsin(\frac{4x}{3}).
  7. Final Answer: Substituting θ\theta back into our integral result gives us:\newline−274⋅arcsin⁡(4x3)+C-\frac{27}{4} \cdot \arcsin\left(\frac{4x}{3}\right) + C\newlineThis is our final answer in terms of xx.

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant