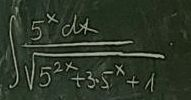int(5^(x)dx)/(sqrt(5^(2x)+3*5^(x)+1))

Question

Bytelearn · Accepted Answer

Simplify Expression: Let's start by simplifying the expression under the square root in the denominator. We can factor the expression as a perfect square trinomial. sqrt(5^(2x) + 3*5^(x) + 1) = sqrt((5^(x) + 1)^2)Rewrite Integral: Now, we rewrite the integral using the simplified expression under the square root. int(5^(x)dx)/(sqrt(5^(2x)+3*5^(x)+1)) = int(5^(x)dx)/(5^(x) + 1)Perform Substitution: We can now perform a substitution to simplify the integral further. Let u = 5^(x) + 1. Then, we need to find du in terms of dx. To find du, we differentiate u with respect to x. du/dx = d/dx(5^(x) + 1) = ln(5)*5^(x) So, du = ln(5)*5^(x)dxExpress dx in Terms: We can now express dx in terms of du and 5^(x). dx = du/(ln(5)*5^(x)) Substitute this expression for dx and u into the integral. int(5^(x)dx)/(5^(x) + 1) = int(5^(x)/(ln(5)*5^(x))du/u)Cancel Terms: Simplify the integral by canceling out the 5^(x) terms. int(5^(x)/(ln(5)*5^(x))du/u) = int(1/(ln(5))du/u)Integrate 1/u: Now we can integrate 1/u with respect to u. int(1/(ln(5))du/u) = (1/ln(5)) * int(1/u du) The integral of 1/u with respect to u is ln|u|.Perform Integration: Perform the integration to find the indefinite integral. (1/ln(5)) * int(1/u du) = (1/ln(5)) * ln|u| + CSubstitute Back: Substitute back the original expression for u to get the final answer. (1/ln(5)) * ln|u| + C = (1/ln(5)) * ln|5^(x) + 1| + C

$\int \frac{5^{x} d x}{\sqrt{5^{2 x}+3 \cdot 5^{x}+1}}$

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

∫5xdx52x+3⋅5x+1 \int \frac{5^{x} d x}{\sqrt{5^{2 x}+3 \cdot 5^{x}+1}} ∫52x+3⋅5x+1​5xdx​

$\int \frac{5^{x} d x}{\sqrt{5^{2 x}+3 \cdot 5^{x}+1}}$