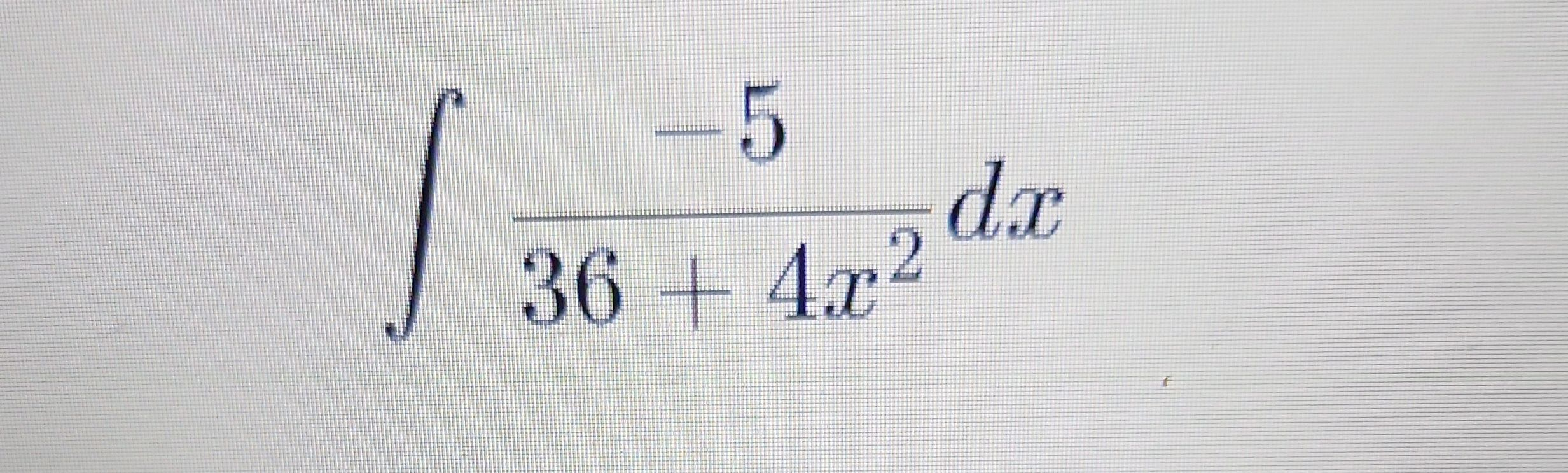AI tutor
Full solution
Q.
Evaluate the integral:
- Given Integral Simplification: We are given the integral: First, we can simplify the integral by factoring out the constant from the denominator: Now, we can pull out the constant from the integral:
- Constant Factor Extraction: Next, we recognize that the integral has the form of the inverse tangent function, where the integral of dx is . In our case, , so . Therefore, we can rewrite the integral as:
- Inverse Tangent Function Integration: Now, we can simplify the constant factor:So the integral becomes: