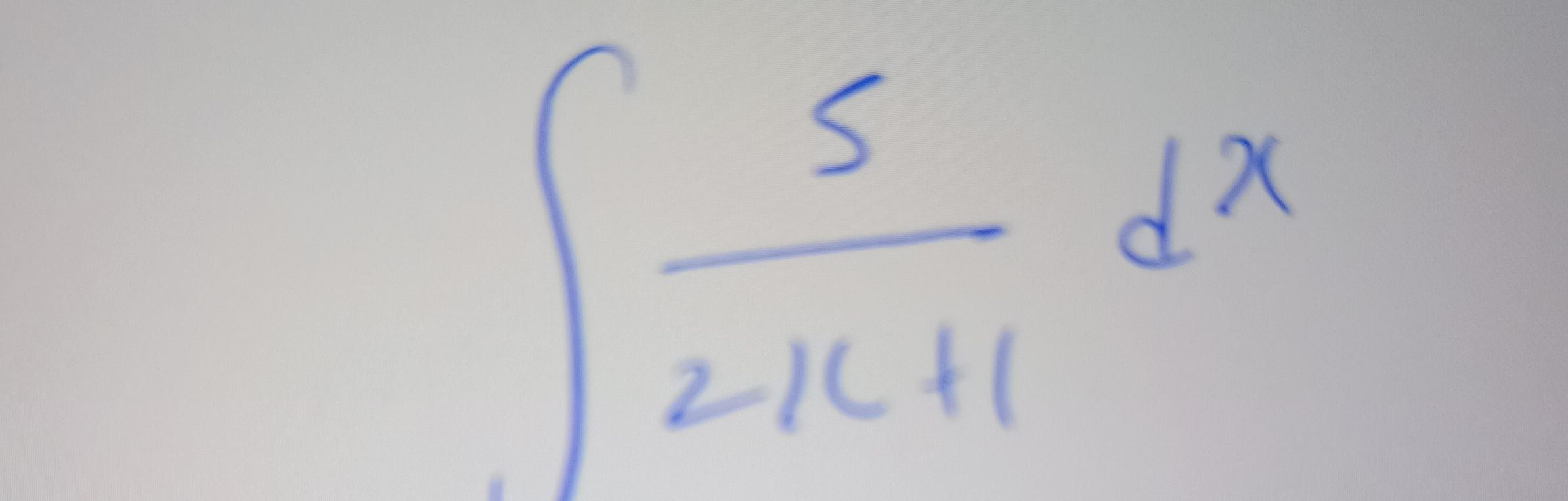AI tutor
Full solution
Q.
- Simplify Integral: Let's simplify the integral: We can factor out the constant :
- Use Substitution: Now, let's use a substitution to make it easier:Let , then .So, .
- Substitute and Simplify: Substitute and simplify:=
- Integrate with Respect: Integrate with respect to :
- Substitute Back: Substitute back for :