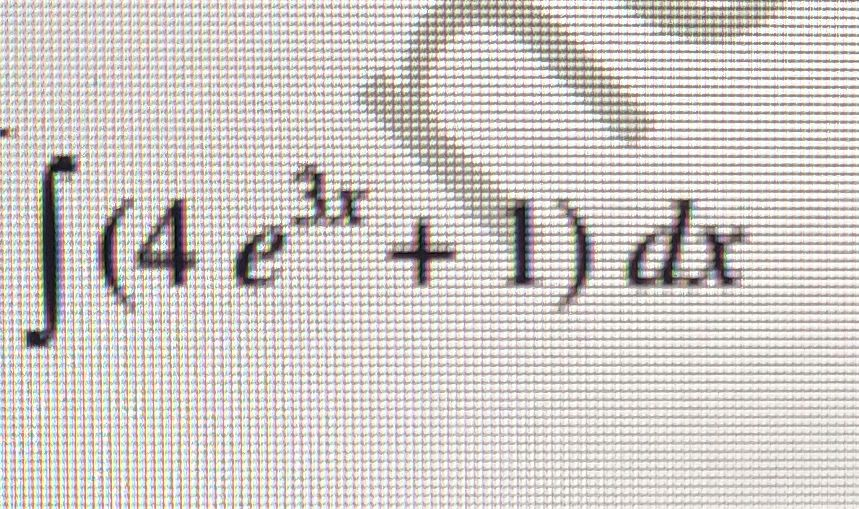Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int(4e^(3x)+1)dx

$\int\left(4 e^{3 x}+1\right) d x$

View step-by-step help

View step-by-step help

Gaussian integral

Full solution

Q.

\int\left(4 e^{3 x}+1\right) d x

Break down into two integrals: Break down the integral into two separate integrals. \int(\(4e^{ $3$ x} + $1$ )\,dx = \int( $4$ e^{ $3$ x})\,dx + \int( $1$ )\,dx
Integrate $4e^{3x}$ : Integrate the first part $\int(4e^{3x})\,dx$ . To integrate $4e^{3x}$ , we use the substitution method. Let $u = 3x$ , which implies $\frac{du}{dx} = 3$ or $dx = \frac{du}{3}$ . Therefore, the integral becomes $\left(\frac{4}{3}\right)\int(e^u)\,du$ .
Perform integration of $e^u$ : Perform the integration of $e^u$ . The integral of $e^u$ with respect to $u$ is $e^u$ . So, $(4/3)\int(e^u)\,du = (4/3)e^u + C$ , where $C$ is the constant of integration.
Substitute back $u = 3x$ : Substitute back $u = 3x$ into the integral. $\newline$ Substituting back, we get $(\frac{4}{3})e^{(3x)} + C$ .
Integrate $1$ : Integrate the second part $\int(1)\,dx$ . The integral of $1$ with respect to $x$ is $x$ . So, $\int(1)\,dx = x + C'$ , where $C'$ is another constant of integration.
Combine results: Combine the results from Step $4$ and Step $5$ . $\newline$ The combined integral is $(\frac{4}{3})e^{(3x)} + x + C''$ , where $C''$ is a new constant of integration that combines $C$ and $C'$ .
Write final answer: Write the final answer. $\newline$ The indefinite integral of the function $4e^{3x} + 1$ with respect to $x$ is $(\frac{4}{3})e^{3x} + x + C$ .

More problems from Gaussian integral

Question

Evaluate the integral.

\newline

\int-x 4^{-3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{3} e^{-2 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int x 5^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-2 x e^{2 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-2 x \cos (-2 x) d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-x \cos (-3 x) d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 5^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-6 x 4^{-4 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 2^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-3 x \sin (-2 x) d x

\newline

Posted 3 months ago