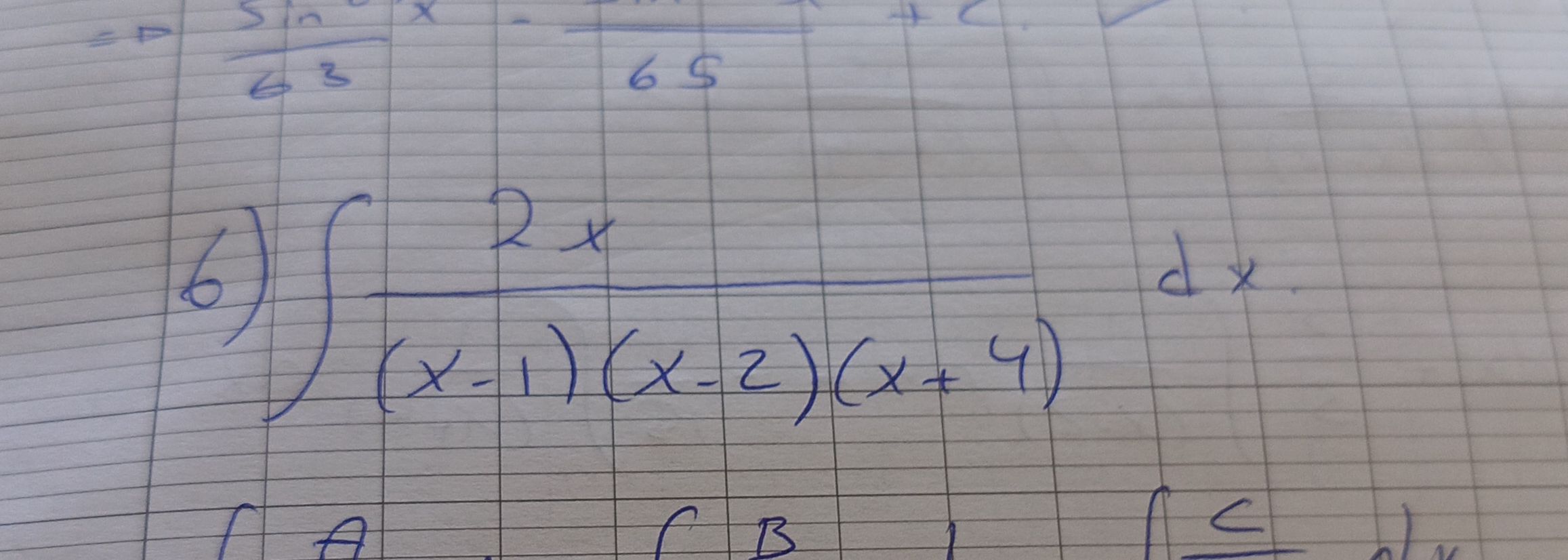int(2x)/((x-1)(x-2)(x+4))dx=

Question

Bytelearn · Accepted Answer

Identify and Decide: Identify the structure of the integral and decide on a strategy. The integral is a rational function where the numerator degree is less than the denominator degree. This suggests that we can use partial fraction decomposition to rewrite the integral as a sum of simpler fractions that can be integrated individually.Perform Decomposition: Perform partial fraction decomposition. We want to express (2x)/((x-1)(x-2)(x+4)) as A/(x-1) + B/(x-2) + C/(x+4), where A, B, and C are constants to be determined.Clear Fractions and Solve: Multiply both sides by the denominator to clear the fractions and solve for A, B, and C. 2x = A(x-2)(x+4) + B(x-1)(x+4) + C(x-1)(x-2) We will now find the values of A, B, and C by plugging in suitable x values that simplify the equation.Find A Value: Find the value of A by plugging in x=1. 2(1) = A(1-2)(1+4) 2 = A(-1)(5) A = -2/5Find B Value: Find the value of B by plugging in x=2. 2(2) = B(2-1)(2+4) 4 = B(1)(6) B = 4/6 B = 2/3Find C Value: Find the value of C by plugging in x=-4. 2(-4) = C(-4-1)(-4-2) -8 = C(-5)(-6) -8 = 30C C = -8/30 C = -4/15Write with Partial Fractions: Write the integral with the determined partial fractions. int(2x)/((x-1)(x-2)(x+4))dx = int(-2/5)/(x-1)dx + int(2/3)/(x-2)dx + int(-4/15)/(x+4)dxIntegrate Each Term: Integrate each term separately. int(-2/5)/(x-1)dx = (-2/5)ln|x-1| + C1 int(2/3)/(x-2)dx = (2/3)ln|x-2| + C2 int(-4/15)/(x+4)dx = (-4/15)ln|x+4| + C3Combine and Write Final Answer: Combine the constants and write the final answer. The final answer is the sum of the three integrals with a single constant of integration. (-2/5)ln|x-1| + (2/3)ln|x-2| + (-4/15)ln|x+4| + C

$\int \frac{2 x}{(x-1)(x-2)(x+4)} d x$ =

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

∫2x(x−1)(x−2)(x+4)dx \int \frac{2 x}{(x-1)(x-2)(x+4)} d x ∫(x−1)(x−2)(x+4)2x​dx=

$\int \frac{2 x}{(x-1)(x-2)(x+4)} d x$ =