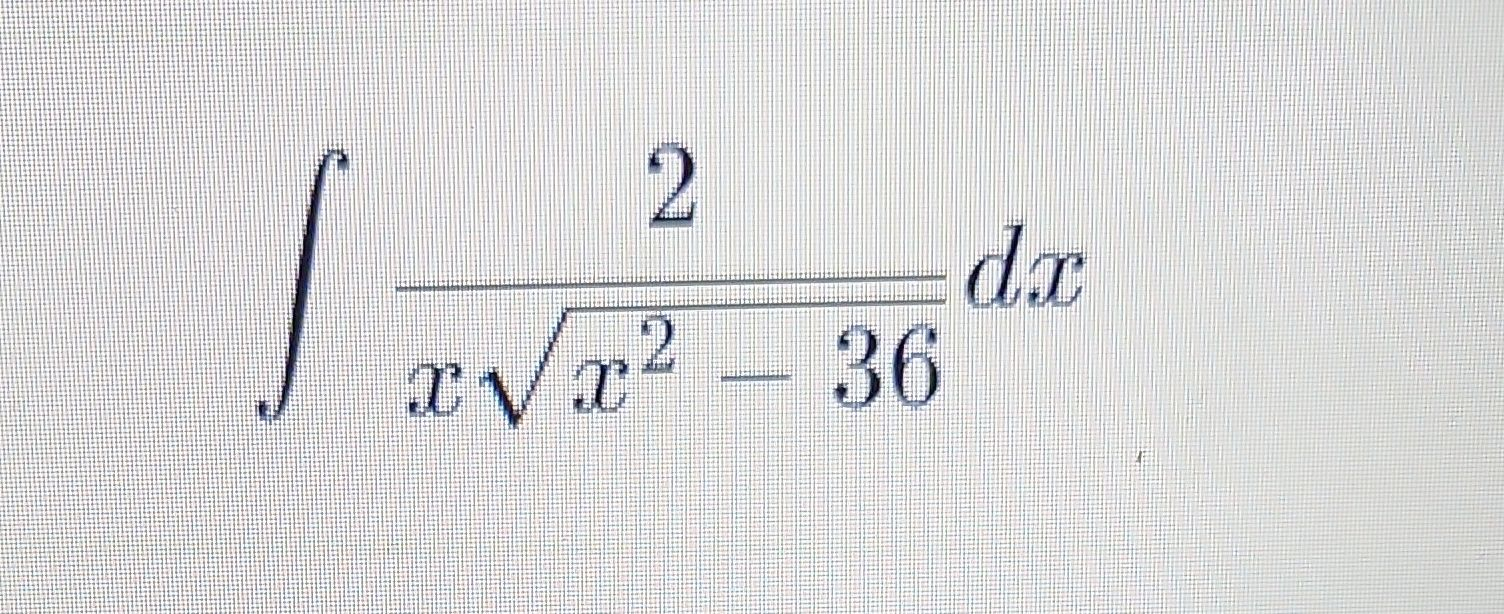Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral: int(2)/(xsqrt(x^(2)-36))dx

Evaluate the integral: $\int \frac{2}{x \sqrt{x^{2}-36}} d x$

View step-by-step help

View step-by-step help

Find indefinite integrals using the substitution and by parts

Full solution

Q. Evaluate the integral:

\int \frac{2}{x \sqrt{x^{2}-36}} d x

Identify Integral: Let's identify the integral we need to solve: $\newline$ $I = \int \frac{2}{x\sqrt{x^2-36}}dx$ $\newline$ We can see that this integral suggests a trigonometric substitution because of the form $a^2 - x^2$ under the square root. We will use the substitution $x = a\sec(\theta)$ , where $a = 6$ in this case, because $36 = 6^2$ .
Substitute $x$ : Substitute $x = 6\sec(\theta)$ into the integral. Then, $dx = 6\sec(\theta)\tan(\theta)d\theta$ and $x^2 - 36 = 36\sec^2(\theta) - 36 = 36(\tan^2(\theta))$ . The integral becomes: $\newline$ $I = \int\frac{2}{6\sec(\theta)\sqrt{36\tan^2(\theta)}} \cdot 6\sec(\theta)\tan(\theta)d\theta$
Simplify Integral: Simplify the integral by canceling terms and using the identity $\sqrt{\tan^2(\theta)} = |\tan(\theta)|$ . Since we are dealing with $x > 6$ (because of the original square root), $\sec(\theta) > 0$ , and thus $\tan(\theta) > 0$ , we can remove the absolute value: $\newline$ $I = \int\frac{2}{6\sec(\theta)\tan(\theta)} \cdot 6\sec(\theta)\tan(\theta)d\theta$ $\newline$ $I = \int 2d\theta$
Integrate with $\theta:$ Integrate with respect to $\theta:$ $I = 2\theta + C$ , where $C$ is the constant of integration.
Substitute back for $\theta$ : We need to substitute back for $\theta$ using our original substitution $x = 6\sec(\theta)$ . We have $\sec(\theta) = \frac{x}{6}$ , and to find $\theta$ , we use the definition of secant: $\sec(\theta) = \frac{1}{\cos(\theta)}$ , so $\cos(\theta) = \frac{6}{x}$ . Then $\theta = \cos^{-1}(\frac{6}{x})$ .
$I = 2\cos^{-1}(\frac{6}{x}) + C$

More problems from Find indefinite integrals using the substitution and by parts

Question

Evaluate the integral.

\newline

\int-x 4^{-3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{3} e^{-2 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int x 5^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-2 x e^{2 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-2 x \cos (-2 x) d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-x \cos (-3 x) d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 5^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-6 x 4^{-4 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int 6 x^{2} 2^{3 x} d x

\newline

Posted 3 months ago

Question

Evaluate the integral.

\newline

\int-3 x \sin (-2 x) d x

\newline

Posted 3 months ago