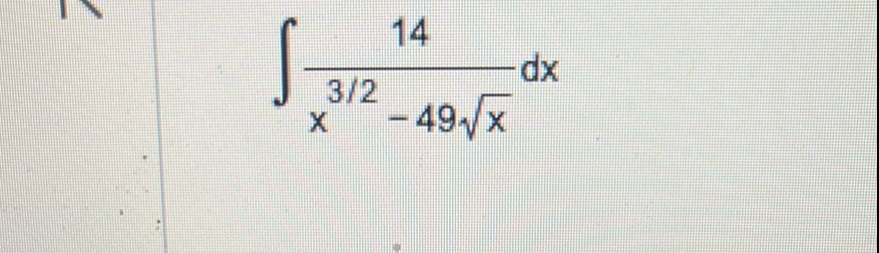int(14)/(x^(3//2)-49sqrtx)dx

Question

Bytelearn · Accepted Answer

Simplify and Substitute: Simplify the integral if possible. We have the integral int(14)/(x^(3/2)-49sqrt(x))dx. We can simplify the denominator by factoring out the common term sqrt(x), which is x^(1/2). x^(3/2) - 49sqrt(x) = sqrt(x)(x - 49) Now, the integral becomes int(14)/(sqrt(x)(x - 49))dx.Alternative Substitution: Perform a substitution. Let u = x - 49, then du/dx = 1, so dx = du. When x = 49, u = 0. We need to change the sqrt(x) in terms of u as well. Since u = x - 49, x = u + 49, and sqrt(x) = sqrt(u + 49). Now, substitute into the integral: int(14)/(sqrt(u + 49) * u)du.New Simplification: Split the integral into two parts if possible. The integral int(14)/(sqrt(u + 49) * u)du is difficult to integrate as it is. However, we can split it into two separate integrals by dividing 14 by the product sqrt(u + 49) * u. This step is not applicable here as the integral does not simplify easily into two separate integrals. We need to find another method to solve this integral.Partial Fraction Decomposition: Look for an alternative substitution or method. The substitution made in Step 2 does not seem to simplify the integral enough for us to integrate easily. We need to consider a different approach. Let's go back to the original integral and try a different substitution. Let's try the substitution u = x^(1/2), which implies x = u^2 and dx = 2u du. Now, substitute into the integral: int(14)/(u^3 - 49u) * 2u du.Integrate with Fractions: Simplify the integral with the new substitution. We have the integral int(14 * 2u)/(u^3 - 49u) du. This simplifies to int(28u)/(u(u^2 - 49)) du. We can cancel out a u from the numerator and denominator: int(28)/(u^2 - 49) du. Now, we have a difference of squares in the denominator: u^2 - 49 = (u - 7)(u + 7).Final Integration: Perform partial fraction decomposition. We can express 1/(u^2 - 49) as A/(u - 7) + B/(u + 7). Multiplying both sides by (u^2 - 49), we get 1 = A(u + 7) + B(u - 7). Setting u = 7, we find that A = 1/14. Setting u = -7, we find that B = -1/14. Now, the integral becomes int(28 * (1/14)/(u - 7) - 1/14/(u + 7)) du.Integrate using the partial fractions. The integral is now int(2/(u - 7) - 2/(u + 7)) du. This integrates to 2ln|u - 7| - 2ln|u + 7| + C.Substitute back to the original variable x. Recall that u = sqrt(x), so the integral becomes 2ln|sqrt(x) - 7| - 2ln|sqrt(x) + 7| + C.

$\int \frac{14}{x^{3 / 2}-49 \sqrt{x}} d x$

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

∫14x3/2−49xdx \int \frac{14}{x^{3 / 2}-49 \sqrt{x}} d x ∫x3/2−49x​14​dx

$\int \frac{14}{x^{3 / 2}-49 \sqrt{x}} d x$