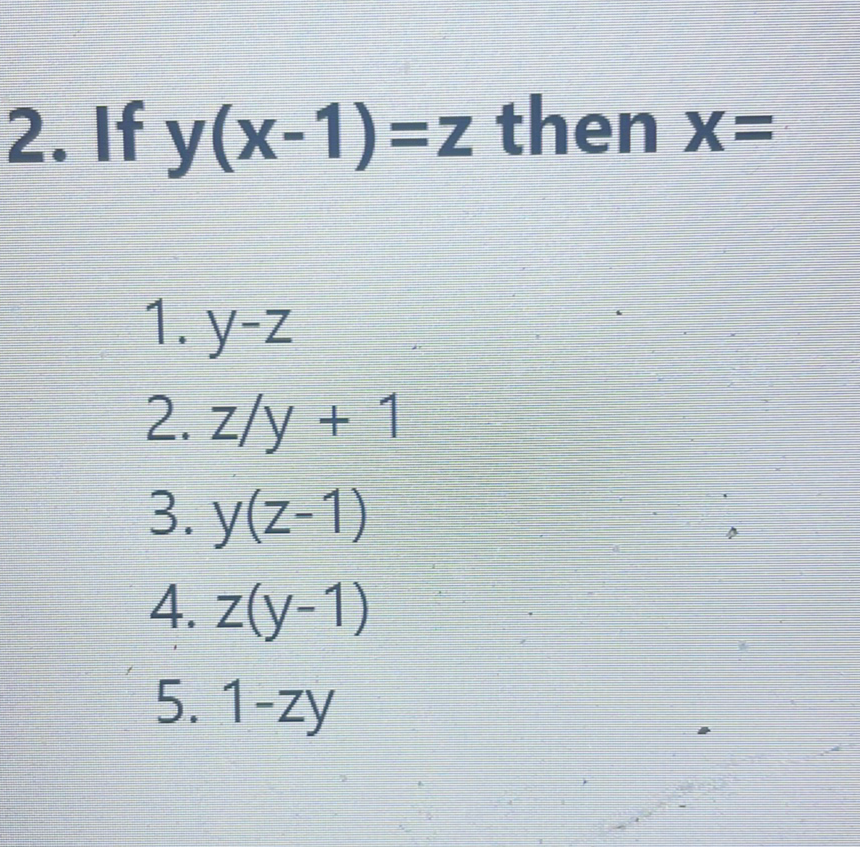Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

If
y(x-1)=z then
x=

y-z

z//y+1

y(z-1)

z(y-1)
1-zy

$2$ . If $y(x-1)=z$ then $x=$ $\newline$ $1$ . $y-z$ $\newline$ $2$ . $z / y+1$ $\newline$ $3$ . $y(z-1)$ $\newline$ $4$ . $z(y-1)$ $\newline$ $5$ . $1$ - $zy$

View step-by-step help

View step-by-step help

Full solution

Q.

2

. If

y(x-1)=z

then

x=

\newline

1

.

y-z

\newline

2

.

z / y+1

\newline

3

.

y(z-1)

\newline

4

.

z(y-1)

\newline

5

.

1

-

zy

Isolate x term: Given the equation $y(x-1)=z$ , we want to solve for $x$ in terms of $y$ and $z$ . First, we isolate the term with $x$ by dividing both sides of the equation by $y$ : $x - 1 = \frac{z}{y}$
Add $1$ to both sides: Next, we add $1$ to both sides of the equation to solve for $x$ : $\newline$ $x = \frac{z}{y} + 1$
Check for matching option: Now we have the expression for $x$ in terms of $y$ and $z$ . We can check the given options to see which one matches our derived expression: $\newline$ $x = \frac{z}{y} + 1$ $\newline$ The correct option that matches this expression is $\frac{z}{y} + 1$ .

More problems from Euler's method

Question

f(x)=x^{3}-6 x^{2}+12 x

c

be the number that satisfies the Mean Value Theorem for

f

on the interval

[0,3]

\newline

c

\newline

1

\newline

0

\newline

1

\newline

2

\newline

3

Posted 2 months ago

Question

g(x)=x^{3}+12 x^{2}+36 x

c

be the number that satisfies the Mean Value Theorem for

g

on the interval

-8 \leq x \leq-2

\newline

c

\newline

1

\newline

-7

\newline

-6

\newline

-3

\newline

-1

Posted 2 months ago

Question

h(x)=x^{3}-6 x^{2}-10 x

c

be the number that satisfies the Mean Value Theorem for

h

on the interval

[-4,5]

\newline

c

\newline

1

\newline

-2

\newline

-1

\newline

1

\newline

3

Posted 1 month ago

Question

g(x)=2 x^{3}-21 x^{2}+60 x

\newline

What is the absolute maximum value of

g

over the closed interval

[0,6]

\newline

1

\newline

25

\newline

42

\newline

36

\newline

52

Posted 1 month ago

Question

f(x)=2 x^{3}+21 x^{2}+36 x

\newline

What is the absolute maximum value of

f

over the closed interval

[-8,0]

\newline

1

\newline

32

\newline

\mathbf{1 8 0}

\newline

\mathbf{1 0 8}

\newline

0

Posted 2 months ago

Question

h(x)=x^{3}+6 x^{2}+2

\newline

What is the absolute minimum value of

h

over the closed interval

-6 \leq x \leq 2

\newline

1

\newline

34

\newline

-34

\newline

2

\newline

-2

Posted 2 months ago

Question

1,000=20z^{2}

\newline

How many distinct real solutions does the given equation have?

\newline

1

\newline

0

\newline

1

\newline

2

\newline

4

Posted 2 months ago

Question

Dante commutes to work

4

mornings a week. For his commute each morning, he walks for

10

minutes, waits and rides the bus for

x

minutes, and waits and rides the train for

y

minutes. If Dante spends at least

3.5

hours on his morning commute each week, which of the following inequalities best describes Dante's weekly morning commute?

\newline

1

\newline

x+y+10 \geq 3.5(60)

\newline

x+y+10 \geq 3.5(60)(4)

\newline

4(x+y)+10 \geq 3.5(60)

\newline

4(x+y+10) \geq 3.5(60)

Posted 2 months ago

Question

\frac{1}{3}x+3y=4

\newline

2x-4=2y

\newline

Consider the given system of equations. If

(x,y)

is the solution to the system, then what is the value of

x-y

\newline

\square

Posted 1 month ago

Question

2

\frac{x}{2}-4=\frac{x}{3}+2

\newline

a) List the title for this type of problem(

10

\newline

b) List the section where you would find nc

\newline

c) List the procedure or rules written in yo

Posted 2 months ago