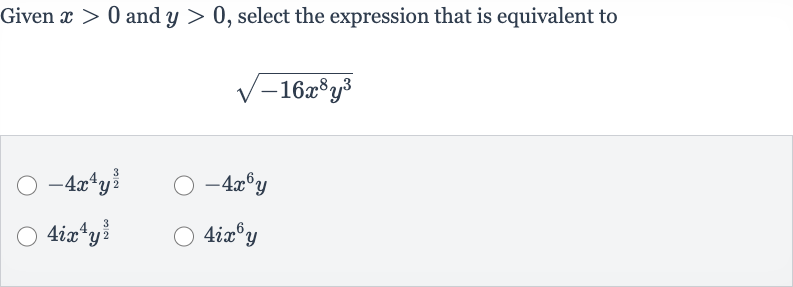Full solution
Q. Given and , select the expression that is equivalent to
- Simplify inside square root: First, we need to simplify the expression inside the square root. The square root of a negative number involves the imaginary unit , where . Therefore, we can rewrite the expression as .
- Simplify square roots: Next, we can simplify the square root of as , and the square root of as , since is a perfect square and and have exponents that are multiples of .
- Multiply simplified expressions: Multiplying these two results together, we get , which simplifies to .
- Check for correct answer: Now we need to check if our result matches any of the given options. The correct expression equivalent to is .