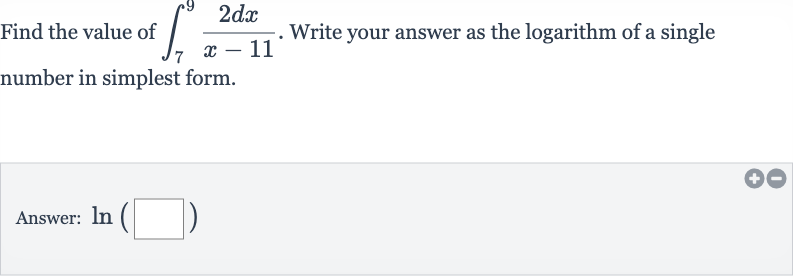
Find the value of int_(7)^(9)(2dx)/(x-11). Write your answer as the logarithm of a single number in simplest form. Answer: ln(◻)

Question

Find the value of  int_(7)^(9)(2dx)/(x-11). Write your answer as the logarithm of a single number in simplest form. Answer:  ln(◻)

Bytelearn · Accepted Answer

Apply Fundamental Theorem: We apply the fundamental theorem of calculus to evaluate the definite integral: ∫_(7)^(9)(2dx)/(x-11) = [2ln|x-11|] from 7 to 9. We substitute the upper and lower limits into the antiderivative: 2ln|9-11| - 2ln|7-11|.Simplify with Substitution: Now we simplify the expression by substituting the values: 2ln|-2| - 2ln|-4|. Since the logarithm of a negative number is not defined in the real number system, we can remove the absolute value bars because both -2 and -4 are negative and will become positive inside the absolute value. This gives us: 2ln(2) - 2ln(4).Further Logarithm Simplification: We can further simplify the expression using logarithm properties: 2ln(2) - 2ln(4) = 2ln(2) - 2ln(2^2). Since ln(2^2) = 2ln(2), the expression becomes: 2ln(2) - 2(2ln(2)).Distribute and Simplify: Now we simplify the expression by distributing the 2 in the second term: 2ln(2) - 4ln(2). This simplifies to: -2ln(2).Final Answer: The final answer is the negative of two times the natural logarithm of 2: Answer: ln(2^(-2)). We can use the property of logarithms that ln(a^b) = b*ln(a) to write the answer as a single logarithm: ln(2^(-2)) = ln(1/4).

Find the value of $\int_{7}^{9} \frac{2 d x}{x-11}$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Find the value of ∫792dxx−11 \int_{7}^{9} \frac{2 d x}{x-11} ∫79​x−112dx​. Write your answer as the logarithm of a single number in simplest form.\newlineAnswer: ln⁡(□) \ln (\square) ln(□)

Find the value of $\int_{7}^{9} \frac{2 d x}{x-11}$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$