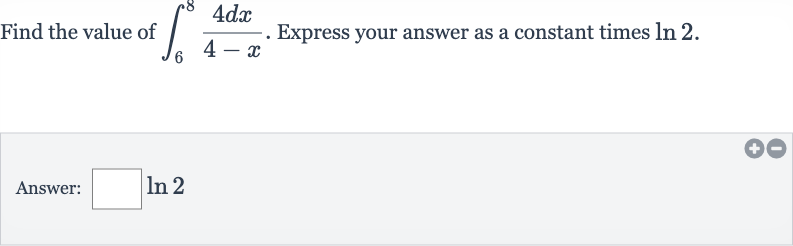
Find the value of int_(6)^(8)(4dx)/(4-x). Express your answer as a constant times ln 2. Answer: ◻ln 2

Question

Find the value of  int_(6)^(8)(4dx)/(4-x). Express your answer as a constant times  ln 2. Answer:  ◻ln 2

Bytelearn · Accepted Answer

Recognize standard form: Recognize the integral as a standard form. The integral $\int \frac{4dx}{4-x}$ can be recognized as a standard form of the integral $\int \frac{A}{B-x}dx$, which can be solved by using the substitution method.Use substitution to simplify: Use substitution to simplify the integral. Let $u = 4-x$, then $du = -dx$. We need to adjust the integral to match this substitution, so we multiply by -1 inside and outside the integral to get $-\int \frac{-4du}{u}$.Rewrite in terms of u: Rewrite the integral in terms of u. The integral now becomes $-4 \int \frac{1}{u} du$, which is a standard form for the natural logarithm function.Integrate with respect to u: Integrate with respect to u. The integral of $\frac{1}{u}$ with respect to u is $\ln|u|$, so the integral becomes $-4 \ln|u| + C$, where C is the constant of integration. However, since we are evaluating a definite integral, we do not need to include the constant of integration.Substitute back in x: Substitute back in terms of x. We originally let $u = 4-x$, so we substitute back to get $-4 \ln|4-x|$.Evaluate definite integral: Evaluate the definite integral from 6 to 8. We need to evaluate $-4 \ln|4-x|$ from 6 to 8. This gives us $-4 [\ln|4-8| - \ln|4-6|]$.Simplify expression: Simplify the expression. We have $-4 [\ln|-4| - \ln|-2|]$, which simplifies to $-4 [\ln(4) - \ln(2)]$.Combine logarithms: Use properties of logarithms to combine the terms. We can use the property $\ln(a) - \ln(b) = \ln(\frac{a}{b})$ to combine the logarithms: $-4 \ln(\frac{4}{2})$.Simplify logarithm: Simplify the logarithm. Since $\frac{4}{2} = 2$, we have $-4 \ln(2)$.Express as constant times ln(2): Express the answer as a constant times $\ln(2)$. The final answer is $-4 \ln(2)$, which is the value of the definite integral from 6 to 8.

Find the value of $\int_{6}^{8} \frac{4 d x}{4-x}$ . Express your answer as a constant times $\ln 2$ . $\newline$ Answer: $\square \ln 2$

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Find the value of ∫684dx4−x \int_{6}^{8} \frac{4 d x}{4-x} ∫68​4−x4dx​. Express your answer as a constant times ln⁡2 \ln 2 ln2.\newlineAnswer: □ln⁡2 \square \ln 2 □ln2

Find the value of $\int_{6}^{8} \frac{4 d x}{4-x}$ . Express your answer as a constant times $\ln 2$ . $\newline$ Answer: $\square \ln 2$