Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of int_(6)^(8)(3)/(x-4)dx. Write your answer as the logarithm of a single number in simplest form. Answer: ln(◻)

Find the value of ∫683x−4dx \int_{6}^{8} \frac{3}{x-4} d x . Write your answer as the logarithm of a single number in simplest form.\newlineAnswer: ln⁡(□) \ln (\square)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

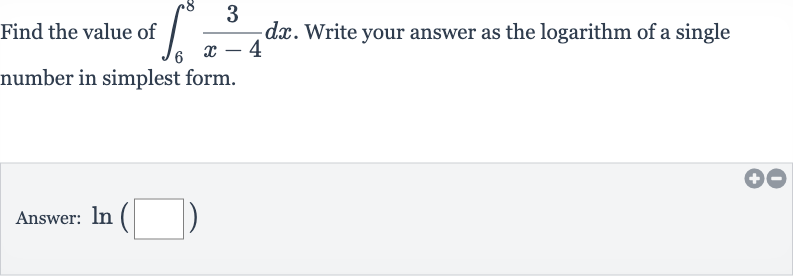
Q. Find the value of ∫683x−4dx \int_{6}^{8} \frac{3}{x-4} d x . Write your answer as the logarithm of a single number in simplest form.\newlineAnswer: ln⁡(□) \ln (\square)
  1. Integrate Function: Now we integrate the function 1x−4\frac{1}{x-4} with respect to xx.\newlineThe antiderivative of 1x−4\frac{1}{x-4} is ln⁡∣x−4∣\ln|x-4|, so the integral from 66 to 88 is:\newline3×[ln⁡∣x−4∣]3 \times [\ln|x-4|] evaluated from 66 to 88
  2. Evaluate Antiderivative: We now evaluate the antiderivative at the upper and lower limits of the integral and subtract the lower evaluation from the upper evaluation.\newline3×[ln⁡∣8−4∣−ln⁡∣6−4∣]3 \times [\ln|8-4| - \ln|6-4|]\newline= 3×[ln⁡∣4∣−ln⁡∣2∣]3 \times [\ln|4| - \ln|2|]\newline= 3×[ln⁡(4)−ln⁡(2)]3 \times [\ln(4) - \ln(2)]
  3. Combine Logarithmic Terms: We can use the properties of logarithms to combine the terms. The difference of logarithms is the logarithm of the quotient of the arguments.\newline3×ln⁡(42)3 \times \ln(\frac{4}{2})\newline= 3×ln⁡(2)3 \times \ln(2)
  4. Apply Power Rule: Since we have a constant multiple of a logarithm, we can use the power rule of logarithms to move the constant inside the logarithm as an exponent.\newlineln⁡(23)\ln(2^3)\newline= ln⁡(8)\ln(8)

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant