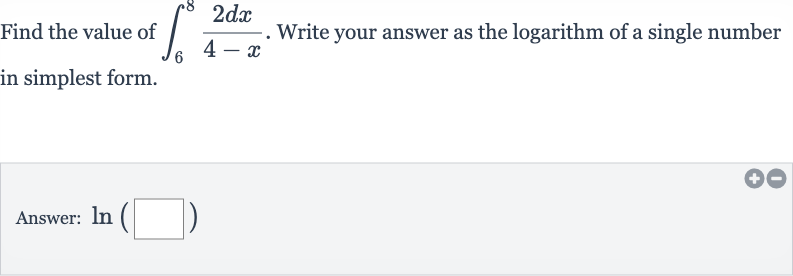
Find the value of int_(6)^(8)(2dx)/(4-x). Write your answer as the logarithm of a single number in simplest form. Answer: ln(◻)

Question

Find the value of  int_(6)^(8)(2dx)/(4-x). Write your answer as the logarithm of a single number in simplest form. Answer:  ln(◻)

Bytelearn · Accepted Answer

Substitution Method: To solve this integral, we can use a substitution method. Let's let u = 4 - x, which means du = -dx. We need to adjust the integral to account for this substitution.Adjusting Integral: Now we substitute u into the integral and adjust the limits of integration. When x = 6, u = 4 - 6 = -2. When x = 8, u = 4 - 8 = -4. Also, we need to substitute -du for dx, which will change the sign of the integral. The integral becomes: ∫ from -2 to -4 of (-2du)/uIntegrating with Respect to u: We can now integrate with respect to u. The integral of -2/u du is -2ln|u|. We will evaluate this from -2 to -4.Evaluating Antiderivative: Evaluating the antiderivative at the bounds gives us: -2ln|-4| + 2ln|-2|Simplifying Expression: Simplify the expression using properties of logarithms. Since the logarithm of a negative number is not defined in the real number system, we can remove the negative signs inside the logarithms because ln|-a| = ln|a| for any positive a. This simplifies to: -2ln(4) + 2ln(2)Further Simplification: Now we use the property of logarithms that ln(a^b) = b*ln(a) to further simplify the expression. This gives us: -2ln(2^2) + 2ln(2)Combining Like Terms: Simplify the expression by applying the power rule for logarithms and combining like terms. This simplifies to: -4ln(2) + 2ln(2)Final Answer: Combine the logarithmic terms to get the final answer. This gives us: -2ln(2)We can now express the final answer as the logarithm of a single number. The final answer is: ln(2^(-2))

Find the value of $\int_{6}^{8} \frac{2 d x}{4-x}$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Find the value of ∫682dx4−x \int_{6}^{8} \frac{2 d x}{4-x} ∫68​4−x2dx​. Write your answer as the logarithm of a single number in simplest form.\newlineAnswer: ln⁡(□) \ln (\square) ln(□)

Find the value of $\int_{6}^{8} \frac{2 d x}{4-x}$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$