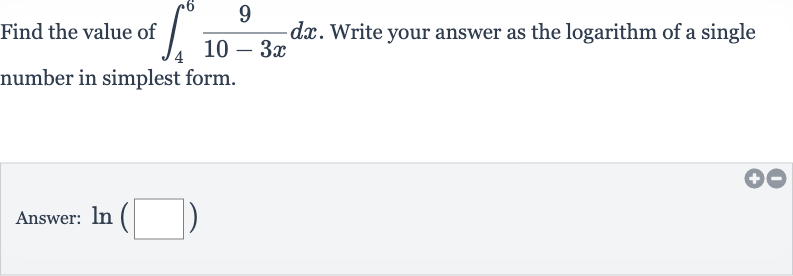
Find the value of int_(4)^(6)(9)/(10-3x)dx. Write your answer as the logarithm of a single number in simplest form. Answer: ln(◻)

Question

Find the value of  int_(4)^(6)(9)/(10-3x)dx. Write your answer as the logarithm of a single number in simplest form. Answer:  ln(◻)

Bytelearn · Accepted Answer

Recognize standard form natural logarithm: Recognize the integral as a standard form of the natural logarithm function. The integral of 1/(a - bx)dx is equal to -1/b * ln|a - bx| + C, where a and b are constants. In our case, a = 10 and b = 3.Apply formula to integral: Apply the formula to the integral. int_(4)^(6)(9)/(10-3x)dx = 9 * int_(4)^(6)1/(10-3x)dx Using the formula from Step 1, we get: = 9 * (-1/3) * ln|10 - 3x| evaluated from 4 to 6.Evaluate natural logarithm at bounds: Evaluate the natural logarithm at the bounds. First, plug in the upper bound (x = 6): ln|10 - 3*6| = ln|10 - 18| = ln|-8| Since the natural logarithm function only takes positive arguments, we use the absolute value to get ln(8).  Next, plug in the lower bound (x = 4): ln|10 - 3*4| = ln|10 - 12| = ln|-2| Similarly, we use the absolute value to get ln(2).  Now we have: 9 * (-1/3) * (ln(8) - ln(2))Simplify the expression: Simplify the expression. 9 * (-1/3) * (ln(8) - ln(2)) = -3 * (ln(8) - ln(2)) Since ln(a) - ln(b) = ln(a/b), we can combine the logarithms: = -3 * ln(8/2) = -3 * ln(4)Express answer as single number: Express the answer as the logarithm of a single number. Since -3 * ln(4) is equivalent to ln(4^(-3)), we can write the final answer as: ln(4^(-3)) = ln(1/64)

Find the value of $\int_{4}^{6} \frac{9}{10-3 x} d x$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Find the value of ∫46910−3xdx \int_{4}^{6} \frac{9}{10-3 x} d x ∫46​10−3x9​dx. Write your answer as the logarithm of a single number in simplest form.\newlineAnswer: ln⁡(□) \ln (\square) ln(□)

Find the value of $\int_{4}^{6} \frac{9}{10-3 x} d x$ . Write your answer as the logarithm of a single number in simplest form. $\newline$ Answer: $\ln (\square)$