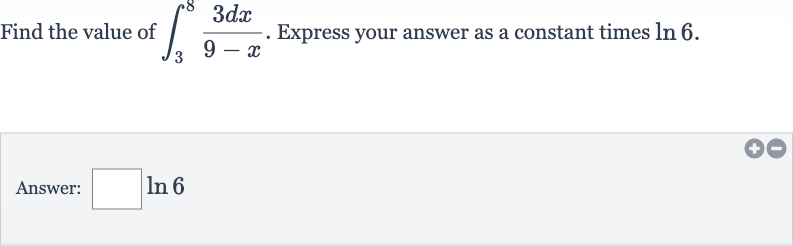
Find the value of int_(3)^(8)(3dx)/(9-x). Express your answer as a constant times ln 6. Answer: ◻ln 6

Question

Find the value of  int_(3)^(8)(3dx)/(9-x). Express your answer as a constant times  ln 6. Answer:  ◻ln 6

Bytelearn · Accepted Answer

Recognize standard form: Recognize the integral as a standard form. The integral $\int \frac{3dx}{9-x}$ can be recognized as a form of the integral $\int \frac{1}{a-x}dx$, which is a standard form whose antiderivative is $-\ln|a-x|$.Substitution with u: Rewrite the integral with a substitution. Let $u = 9-x$, then $du = -dx$. We need to adjust the integral to match this substitution, so we multiply by -1 inside and outside the integral to get $-3\int \frac{du}{u}$.Change limits of integration: Change the limits of integration. When $x = 3$, $u = 9-3 = 6$. When $x = 8$, $u = 9-8 = 1$. So the new limits of integration are from $u = 6$ to $u = 1$.Perform integration: Perform the integration. The integral $-3\int \frac{du}{u}$ from $u = 6$ to $u = 1$ is $-3[\ln|u|]_6^1$.Evaluate definite integral: Evaluate the definite integral. Plugging in the limits of integration, we get $-3[\ln|1| - \ln|6|]$. Since $\ln|1| = 0$, this simplifies to $-3[-\ln|6|]$.Simplify expression: Simplify the expression. The expression $-3[-\ln|6|]$ simplifies to $3\ln|6|$, which is $3\ln 6$ because the absolute value of a positive number is the number itself.

Find the value of $\int_{3}^{8} \frac{3 d x}{9-x}$ . Express your answer as a constant times $\ln 6$ . $\newline$ Answer: $\square \ln 6$

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Find the value of ∫383dx9−x \int_{3}^{8} \frac{3 d x}{9-x} ∫38​9−x3dx​. Express your answer as a constant times ln⁡6 \ln 6 ln6.\newlineAnswer: □ln⁡6 \square \ln 6 □ln6

Find the value of $\int_{3}^{8} \frac{3 d x}{9-x}$ . Express your answer as a constant times $\ln 6$ . $\newline$ Answer: $\square \ln 6$