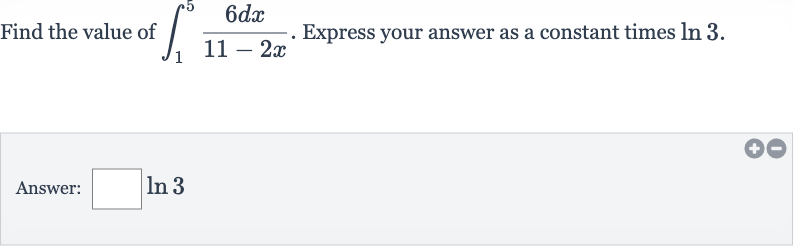
Find the value of int_(1)^(5)(6dx)/(11-2x). Express your answer as a constant times ln 3. Answer: ◻ln 3

Question

Find the value of  int_(1)^(5)(6dx)/(11-2x). Express your answer as a constant times  ln 3. Answer:  ◻ln 3

Bytelearn · Accepted Answer

Identify Integral: Let's first identify the integral we need to solve: I = ∫ from 1 to 5 of (6dx)/(11-2x) We can start by performing a u-substitution where u = 11 - 2x, which means du = -2dx.Perform u-Substitution: Now we solve for dx in terms of du: dx = -du/2 We also need to change the limits of integration. When x = 1, u = 11 - 2(1) = 9. When x = 5, u = 11 - 2(5) = 1.Solve for dx: Substitute u and dx into the integral: I = ∫ from u=9 to u=1 of (6(-du/2))/u This simplifies to: I = -3 ∫ from u=9 to u=1 of du/uChange Limits of Integration: We can now integrate with respect to u: I = -3 [ln|u|] from u=9 to u=1Substitute u and dx: Now we apply the limits of integration: I = -3 [ln|1| - ln|9|] Since ln|1| = 0, this simplifies to: I = -3 [-ln|9|]Integrate with Respect to u: We know that ln|9| = ln(3^2) = 2ln(3), so we can substitute this in: I = -3 [-2ln(3)] I = 6ln(3)Apply Limits of Integration: Finally, we express the answer as a constant times ln 3: I = 6ln(3)

Find the value of $\int_{1}^{5} \frac{6 d x}{11-2 x}$ . Express your answer as a constant times $\ln 3$ . $\newline$ Answer: $\square \ln 3$

Full solution

More problems from Find indefinite integrals using the substitution and by parts

Related topics

Find the value of ∫156dx11−2x \int_{1}^{5} \frac{6 d x}{11-2 x} ∫15​11−2x6dx​. Express your answer as a constant times ln⁡3 \ln 3 ln3.\newlineAnswer: □ln⁡3 \square \ln 3 □ln3

Find the value of $\int_{1}^{5} \frac{6 d x}{11-2 x}$ . Express your answer as a constant times $\ln 3$ . $\newline$ Answer: $\square \ln 3$