Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the
8^("th ") term in the sequence

-(1)/(2),-1,-2,-4,dots
Hint: Write a formula to help you.

Find the $8^{\text{th}}$ term in the sequence $\newline$ $-\frac{1}{2},-1,-2,-4,\dots$ $\newline$ Hint: Write a formula to help you.

View step-by-step help

View step-by-step help

Find indefinite integrals using the substitution

Full solution

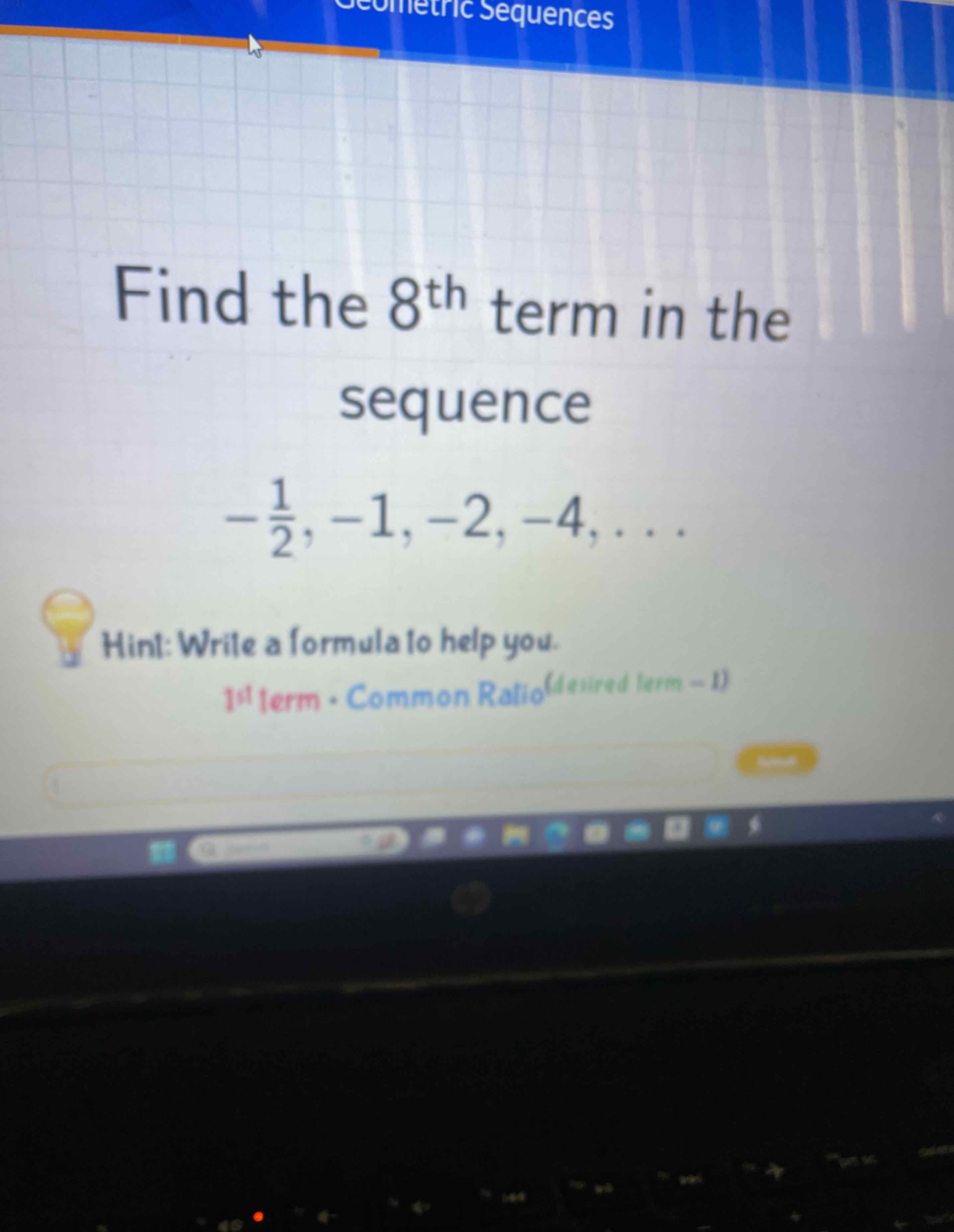
Q. Find the

8^{\text{th}}

term in the sequence

\newline

-\frac{1}{2},-1,-2,-4,\dots

\newline

Hint: Write a formula to help you.

Identify pattern: Step $1$ : Identify the pattern in the sequence. $\newline$ The sequence given is $-1$ / $2$ , $-1$ , $-2$ , $-4$ , ... $\newline$ Notice that each term is twice the previous term. This is a geometric sequence with the first term $a = -\frac{1}{2}$ and the common ratio $r = 2$ .
Write formula: Step $2$ : Write the formula for the nth term of a geometric sequence. $\newline$ The nth term $a_n$ of a geometric sequence can be found using the formula: $\newline$ $a_n = a \cdot r^{(n-1)}$ $\newline$ where $a$ is the first term and $r$ is the common ratio.
Substitute values: Step $3$ : Substitute the values into the formula to find the $8$ th term. $\newline$ Using the formula from Step $2$ : $\newline$ $a_8 = -\frac{1}{2} \cdot 2^{(8-1)}$ $\newline$ $a_8 = -\frac{1}{2} \cdot 2^7$ $\newline$ $a_8 = -\frac{1}{2} \cdot 128$ $\newline$ $a_8 = -64$

More problems from Find indefinite integrals using the substitution

Question

\frac{d^{2}}{d x^{2}}\left[5 \ln \left(x^{5}\right)\right]

Posted 3 months ago

Question

Consider the curve given by the equation

x y^{2}-x^{3} y=8

. It can be shown that

\frac{d y}{d x}=\frac{3 x^{2} y-y^{2}}{2 x y-x^{3}}

\newline

Write the equation of the vertical line that is tangent to the curve.

Posted 3 months ago

Question

Consider the curve given by the equation

2 x^{2}-12 x+y^{3}=107

. It can be shown that

\frac{d y}{d x}=\frac{4(3-x)}{3 y^{2}}

\newline

Find the point on the curve where the line tangent to the curve is horizontal.

\newline

(\square

\square)

Posted 3 months ago

Question

Can this differential equation be solved using separation of variables?

\newline

\frac{d y}{d x}=\frac{3}{x^{2} y-8 y}

\newline

1

\newline

\newline

Posted 3 months ago

Question

\begin{array}{c}y=x^{4} \\ \frac{d y}{d x}=\end{array}

Posted 3 months ago

Question

Solve the equation. Check your solution

\newline

19=2-(z+5)

\newline

The solution set is \(\{\longrightarrow\}. (Simplify your answer

Posted 2 months ago

Question

\int \frac{t^{2}}{\sin(1-t^{3})\tan(1-t^{3})} \, dt

Posted 2 months ago

Question

Write the answer in proper scientific notation:

\newline

(8 \times 10^{5} \times 10^{-7})^{4}

Posted 2 months ago

Question

x

and graph the solution on the number line below.

\newline

\frac{x}{-2} < 0

\newline

1

2

\newline

<

\newline

\geq

\newline

\geq

\newline

Inequality Notation:

\newline

Posted 2 months ago

Question

-\int \frac{t^{4}}{(1-t^{2})^{2}} \, dt

Posted 2 months ago