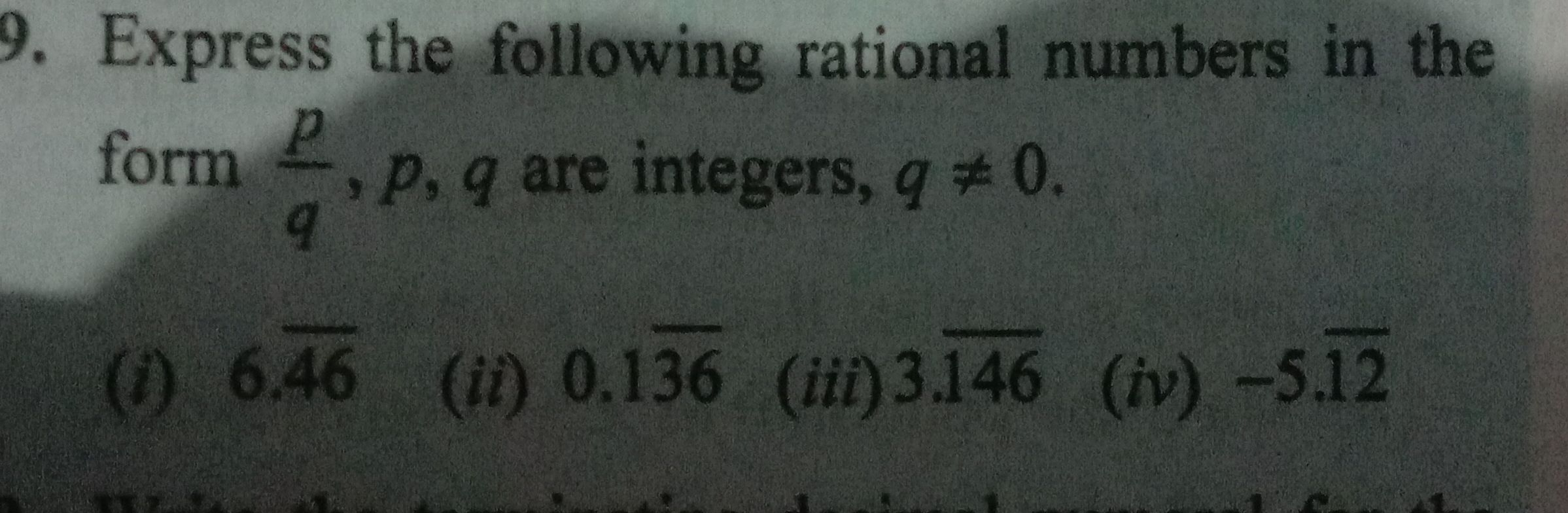
Express the following rational numbers in the form $\frac{p}{q}, p, q$ are integers, $q \neq 0$ . $\newline$ (i) $6 . \overline{46}$ $\newline$ (ii) $0 . \overline{136}$ $\newline$ (iii) $3 . \overline{146}$ $\newline$ (iv) $-5 . \overline{12}$

View step-by-step help

Home

Math Problems

Calculus

Euler's method

Full solution

Q. Express the following rational numbers in the form

\frac{p}{q}, p, q

are integers,

q \neq 0

\newline

(i)

6 . \overline{46}

\newline

(ii)

0 . \overline{136}

\newline

(iii)

3 . \overline{146}

\newline

(iv)

-5 . \overline{12}

Set Variable $x$ : To convert a repeating decimal to a fraction, we let the repeating decimal be equal to a variable, say $x$ . For example, if we have $6.\overline{46}$ , we can write $x = 6.464646\ldots$
Multiply by Power of $10$ : Next, we multiply $x$ by a power of $10$ that matches the length of the repeating pattern to shift the decimal point to the right, just before the pattern starts repeating again. For $6.\overline{46}$ , the repeating pattern is $46$ , which is two digits long, so we multiply by $10^2$ (which is $100$ ). We get $100x = 646.464646\ldots$
Subtract to Eliminate Decimals: Now, we subtract the original $x$ from this new equation to get rid of the repeating decimals. So, $100x - x = 646.464646... - 6.464646...$ This gives us $99x = 640$ .
Solve for x: We then solve for x by dividing both sides of the equation by $99$ . So, $x = \frac{640}{99}$ . This fraction can be simplified if necessary.
Convert to Fraction: For $6.\overline{46}$ , the simplified fraction is $x = \frac{640}{99}$ , which cannot be simplified further. So, the fraction form of $6.\overline{46}$ is $\frac{640}{99}$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ . For $10^3$ $0$ , let $10^3$ $1$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ . For $10^3$ $0$ , let $10^3$ $1$ Multiply $x$ by $10^3$ $3$ (which is $10^3$ $4$ ) because the repeating pattern $10^3$ $5$ is two digits long. We get $10^3$ $6$
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ . For $10^3$ $0$ , let $10^3$ $1$ Multiply $x$ by $10^3$ $3$ (which is $10^3$ $4$ ) because the repeating pattern $10^3$ $5$ is two digits long. We get $10^3$ $6$ Subtract the original $x$ from this new equation: $10^3$ $8$ This gives us $10^3$ $9$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ . For $10^3$ $0$ , let $10^3$ $1$ Multiply $x$ by $10^3$ $3$ (which is $10^3$ $4$ ) because the repeating pattern $10^3$ $5$ is two digits long. We get $10^3$ $6$ Subtract the original $x$ from this new equation: $10^3$ $8$ This gives us $10^3$ $9$ . Solve for $x$ by dividing both sides by $1000$ $1$ . So, $1000$ $2$ . This fraction can be simplified by dividing both numerator and denominator by $1000$ $3$ . So, $1000$ $4$ .
Repeat for Other Decimals: We repeat the process for $0.\overline{136}$ . Let $x = 0.136136136\ldots$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $136$ is three digits long. We get $1000x = 136.136136\ldots$ Subtract the original $x$ from this new equation: $1000x - x = 136.136136\ldots - 0.136136\ldots$ This gives us $999x = 136$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x = 0.136136136\ldots$ $2$ . This fraction cannot be simplified further. So, the fraction form of $0.\overline{136}$ is $x = 0.136136136\ldots$ $4$ . For $x = 0.136136136\ldots$ $5$ , let $x = 0.136136136\ldots$ $6$ Multiply $x$ by $10^3$ (which is $1000$ ) because the repeating pattern $x$ $0$ is three digits long. We get $x$ $1$ Subtract the original $x$ from this new equation: $x$ $3$ This gives us $x$ $4$ . Solve for $x$ by dividing both sides by $x = 0.136136136\ldots$ $1$ . So, $x$ $7$ . This fraction can be simplified by dividing both numerator and denominator by $x$ $8$ . So, $x$ $9$ . For $10^3$ $0$ , let $10^3$ $1$ Multiply $x$ by $10^3$ $3$ (which is $10^3$ $4$ ) because the repeating pattern $10^3$ $5$ is two digits long. We get $10^3$ $6$ Subtract the original $x$ from this new equation: $10^3$ $8$ This gives us $10^3$ $9$ . Solve for $x$ by dividing both sides by $1000$ $1$ . So, $1000$ $2$ . This fraction can be simplified by dividing both numerator and denominator by $1000$ $3$ . So, $1000$ $4$ . We have now converted all the given repeating decimals to fractions. The final answers are: (i) $1000$ $5$ (ii) $1000$ $6$ (iii) $1000$ $7$ (iv) $1000$ $8$