AI tutor
Full solution
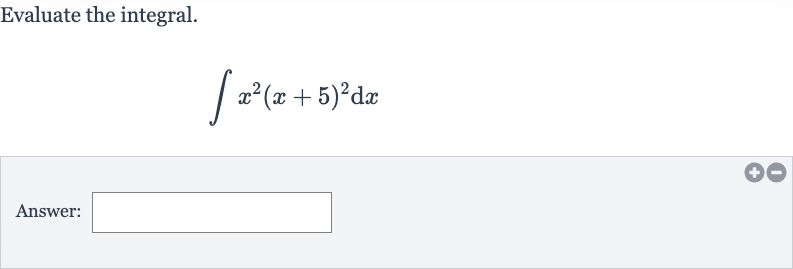
Q. Evaluate the integral.Answer:
- Expand Integrands: To evaluate the integral of , we first expand the integrand to make the integration process straightforward.
- Integrate Each Term: Now we integrate each term separately.
- Simplify Final Answer: We simplify the expression to get the final answer.